1. ESQUEMAS

2. PRESENTACIONES

Principio de Arquímedes. Presiones en fluidos
3. CONTENIDOS ANIMADOS







4. INTRODUCCIÓN
La Dinámica es una parte de la Física que estudia las acciones que se ejercen sobre los cuerpos y la manera en que estas acciones influyen sobre el movimiento de los mismos.
¿Por qué un cuerpo modifica su velocidad?
Un cuerpo modifica su velocidad si sobre él se ejerce una acción externa.
Las acciones externas se representan por fuerzas.
La variación de la velocidad viene medida por la aceleración.
Luego si sobre un cuerpo se ejerce una fuerza, éste modifica su velocidad. Las fuerzas producen variaciones en la velocidad de los cuerpos. Las fuerzas son las responsables de las aceleraciones.
La eficacia de una fuerza para producir un giro depende de:
- La intensidad de la fuerza (F).
- La distancia entre el eje de giro y la dirección en que actúa la fuerza (d).

- Módulo: el producto del módulo de la fuerza (F) por la distancia entre el eje de giro y la dirección de la fuerza (d).
- Dirección: perpendicular al plano que definen la fuerza y el punto.
- Sentido: positivo si el giro se produce en sentido contrario a las agujas del reloj y negativo si el giro se produce en el mismo sentido de las agujas del reloj.
La unidad de fuerza usada en el S.I. es el Newton (N)
| Para medir fuerzas se usan los aparatos llamados dinamómetros. En el Sistema Internacional, la unidad de fuerza es el newton, cuyo símbolo es N. Un newton es la fuerza que aplicada a una masa de 1 kilogramo la acelera 1 m/s2 |
La fuerza es una magnitud vectorial. Además de su intensidad o módulo, una fuerza se caracteriza por su dirección y sentido.
¿Cómo se pueden determinar las fuerzas que actúan sobre un cuerpo?
La respuesta es muy sencilla:
Se determinan las acciones externas sobre el cuerpo. Cada acción se representa por una fuerza.
Hay que tener claro que sobre un cuerpo se actúa mediante contacto físico con él (empujándolo, tirando con una cuerda…) y una vez que deja de existir el contacto, cesa la acción y, por tanto, la fuerza deja de actuar.
De esta regla tenemos que hacer (en este curso) una excepción: la gravedad. Como consecuencia de que vivimos en el planeta Tierra, éste ejerce una atracción sobre los cuerpos. La fuerza de gravedad actúa siempre.
4.1. Composición y descomposición de una fuerza
Para resolver muchos problemas resulta útil descomponer una fuerza en otras dos en la dirección de los ejes de coordenadas cuyos efectos sumados son iguales a la propia fuerza.
Las proyecciones sobre los ejes son sus componentes.
Aplicando la definición de seno y de coseno al ángulo que forma el vector con el eje x, podemos calcular las componentes:
Fx = F· cos(a) ; Fy = F· sen(a)
5. ¿QUÉ ES UNA FUERZA?
En nuestra vida cotidiana usamos a menudo la palabra fuerza. Por ejemplo:
- Si una cosa cae al suelo, decimos que es debido a la fuerza de la gravedad.
- Si enfrentamos dos imanes decimos que la repulsión o la atracción entre ellos es debida a la fuerza magnética.
- Al empujar una cosa para moverla también decimos que hacemos fuerza.
- Y lo mismo si apretamos un balón hasta deformarlo o estiramos un muelle.
- Y también hacemos fuerza si sostenemos algo para que no se caiga al suelo. Estos ejemplos son casos muy distintos. Entonces, ¿qué es una fuerza?
5.1. Concepto de fuerza
Las fuerzas son los agentes que la física utiliza para explicar las interacciones entre los cuerpos, es decir, lo que le ocurre a un cuerpo debido a la presencia cercana o lejana de otro cuerpo (Figura 1.1). Estas interacciones pueden ser:
Los resultados de la acción de una fuerza son de dos tipos:
|
Si las fuerzas que actúan están igualadas, se anulan y no consiguen resultados.
Cuando la fuerza que ejercemos iguala pero no consigue superar a otras fuerzas, no hay resultados netos.
Una de estas fuerzas es la fuerza de rozamiento.

Las fuerzas pueden ser de dos tipos, de contacto o a distancia.
Fuerzas de contacto son aquellas que actúan solamente cuando es necesario el contacto físico entre los elementos que interaccionan. Ejemplo: cuando se golpea una pelota con una raqueta.
Fuerzas a distancia se producen sin necesidad de contacto físico entre los cuerpos que interaccionan. Ejemplo: la fuerza que ejerce la Tierra sobre un cuerpo y que hace que tienda a caer sobre ella si se encuentra en el aire. Esa fuerza se llama peso.
Figura 1. Los cuerpos acelerandebido a las fuerzas.
|
Figura 2. Los cuerpos cambian de formadebido a las fuerzas.
|
ANIMACIONES
6. ADICIÓN DE FUERZAS
| Si dos o más fuerzas actúan sobre el mismo objeto, con el mismo punto de aplicación y la misma dirección pueden sumarse fácilmente obteniendo la resultante, . 6.1. Si tienen la misma dirección y sentido, sus valores se suman para hallar la fuerza resultante , que también tiene la misma dirección y sentido:
| . |
6.3. Las dos fuerzas tienen direcciones perpendiculares
 6.4. Par de fuerzas
6.4. Par de fuerzas Cuando un conductor utiliza una llave para quitar la rueda de un coche, aplica dos fuerzas iguales y de sentidos contrarios.
Se observa que la llave no experimenta movimiento de traslación alguno, es decir, no se desplaza, pero sí gira bajo la acción del par de fuerzas.

La resultante de un par de fuerzas es nula, pero el momento resultante no lo es.
El efecto de giro producido por un par de fuerzas se mide mediante el momento del par. Su módulo es igual al producto del módulo de una de las fuerzas (F) por la distancia entre las rectas sobre las que actúa cada una de ellas, distancia que se denomina brazo del par (d).
 Dos fuerzas iguales y de sentidos contrarios actuando en el mismo cuerpo constituyen un par de fuerzas y producen un momento que causa su giro.
Dos fuerzas iguales y de sentidos contrarios actuando en el mismo cuerpo constituyen un par de fuerzas y producen un momento que causa su giro.
El efecto de giro producido por un par de fuerzas se mide mediante el momento del par. Su módulo es igual al producto del módulo de una de las fuerzas (F) por la distancia entre las rectas sobre las que actúa cada una de ellas, distancia que se denomina brazo del par (d).
M = F ·d
 Dos fuerzas iguales y de sentidos contrarios actuando en el mismo cuerpo constituyen un par de fuerzas y producen un momento que causa su giro.
Dos fuerzas iguales y de sentidos contrarios actuando en el mismo cuerpo constituyen un par de fuerzas y producen un momento que causa su giro. 6.5. El equilibrio de los cuerpos
6.5. El equilibrio de los cuerpos
Un sólido está en equilibrio estático cuando no realiza movimiento alguno, ni de traslación ni de rotación, es decir, cuando ni se desplaza ni gira.
Para que un sólido, inicialmente en reposo, no se mueva, se deben cumplir las siguientes condiciones:
Para que un sólido, inicialmente en reposo, no se mueva, se deben cumplir las siguientes condiciones:
- No debe actuar sobre él ninguna fuerza. Esto ya sabemos que en la práctica es imposible, pero sí debe ocurrir que la resultante de todas las fuerzas que actúan sobre el cuerpo sea nula. Esta es la condición necesaria para que el sólido no se desplace. R = 0
- Pero aunque la resultante de las fuerzas que actúan sobre él sea cero y el cuerpo no se desplace, sí podría girar. Para que no gire es necesario que el momento resultante de las fuerzas que actúan sobre él sea nulo. M = 0
Por ejemplo, vamos a ver qué ocurre cuando una balanza romana alcanza el equilibrio:
Equilibrio en una balanza romana
La romana es una balanza de brazos desiguales que se utiliza para medir masas. Consta de una barra que oscila en torno a un punto de suspensión, un platillo en el que se pone el objeto que se vaya a pesar y una pesa patrón.
El equilibrio se alcanza cuando la barra permanece horizontal; esto es, cuando la suma de los momentos de todas las fuerzas que actúan sobre la barra respecto del punto de suspensión es cero.
 M = 0 masa objeto · g · a = masa pesa · g · b masa objeto · a = masa pesa · b
M = 0 masa objeto · g · a = masa pesa · g · b masa objeto · a = masa pesa · b
Equilibrio en una balanza romana
La romana es una balanza de brazos desiguales que se utiliza para medir masas. Consta de una barra que oscila en torno a un punto de suspensión, un platillo en el que se pone el objeto que se vaya a pesar y una pesa patrón.
El equilibrio se alcanza cuando la barra permanece horizontal; esto es, cuando la suma de los momentos de todas las fuerzas que actúan sobre la barra respecto del punto de suspensión es cero.
 M = 0 masa objeto · g · a = masa pesa · g · b masa objeto · a = masa pesa · b
M = 0 masa objeto · g · a = masa pesa · g · b masa objeto · a = masa pesa · b
Supuesto práctico 1
| Sobre un bloque actúan las fuerzas que están indicadas en la Figura 8. Calcula la fuerza resultante. De las tres fuerzas que actúan sobre el cuerpo →F2 y →F3 tienen el mismo sentido y →F1 sentido contrario. Consideramos positivas las que apuntan hacia la derecha y negativa la otra. Su suma será: →F1+→F2 + →F3 = -12 N + 8 N + 4 N = 0 N El cuerpo estará en equilibrio. Las fuerzas se anulan. Nota: Las flechas van justo encima de la F, pero no se puede escribis así en HTML. (Lenguaje de página web).
6.6. Fuerzas concurrentes
Dos fuerzas concurrentes se suman como vimos en el apartado de composición de fuerzas. Si existen más de dos fuerzas, se hallan las proyecciones sobre los ejes de todas y se suman aritméticamente estas componentes. Se aplica el T. de Pitágoras a estas resultantes tomadas como catetos. La hipotenusa será la resultante final (define su dirección, módulo y sentido). Para neutralizar fuerzas concurrentes aplicadas en un punto, O, de un sólido rígido, debemos situar en ese punto una fuerza de igual valor y opuesta a la resultante: Fequilibrante. Entonces: F1+F2+F3 + Fequilib= 0; No hay desplazamiento Como el sólido en el que actúan es un punto no hay giro: M = F·d, si d = 0 entonce M = 0. 6.7. Fuerzas paralelas de igual sentido La fuerza resultante es una fuerza, FR de: Intensidad (módulo) suma de los módulos de F1 y F2. Dirección paralela a F1 y F2 Sentido el de las fuerzas. Punto de aplicación situado en el segmento que une los puntos de aplicación de F1 y F2y lo divide en dos partes, x1 y x2, inversamente proporcionales a los módulos de F1 y F2 (la fuerza mayor está al lado de la parte menor de las x1 y x2). La fuerza que las equilibra es igual y opuesta a la fuerza resultante (Fequilibrante= - FR). Equilibrio de traslación: SF = 0; R- F1-F2=0 Equilibrio rotación: SM = 0; F1·x1- F2·x2=0   La fuerza resultante es una fuerza, Fr de: Intensidad (módulo) diferencia de los módulos de F1 y F2. Dirección paralela a F1 y F2 Sentido el de la fuerza mayor. Punto de aplicación situado en la prolongación del segmento que une los puntos de aplicación de F1 y F2 y su distancia a éstas es inversamente proporcional a los módulos de F1 y F2. (Está fuera del segmento de unión y del lado de la fuerza mayor). La fuerza que las equilibra es igual y opuesta a la fuerza resultante (F
equilibrante= - Fr).
Para equilibrar el giro, el momento de F1 y F2 respecto a O debe anularse. F1· x1 - F2· (d+x1) = 0 |










 7. PALANCAS Y POLEAS
7. PALANCAS Y POLEASEl hombre ha tenido que recurrir al ingenio para conseguir multiplicar su capacidad de acción sobre los cuerpos. Las máquinas son dispositivos utilizados para transformar las fuerzas que se aplican sobre ellos. Las que constan de un solo componente se llaman máquinas simples, como la palanca y la polea.
La fuerza aplicada a la máquina se denomina potencia y la fuerza que se trata de vencer, la que la máquina aplica al cuerpo sobre el que actúa, resistencia.
La palanca es una máquina simple que transmite la fuerza que se aplica en un punto a otro punto en el que se obtiene una fuerza mayor.
La polea es una máquina simple que nos puede ayudar a subir pesos ahorrando esfuerzo.
| |||||||||||
 7.1. Clases de palancas Hemos visto que las palancas son cuerpos rígidos que giran alrededor de un punto de apoyo, llamado fulcro. Según la localización del punto de apoyo respecto a los puntos de aplicación de la potencia y de la resistencia, hay tres géneros de palancas: |
| |||||||||||||
ANIMACIONES
8. LAS FUERZAS CAMBIAN LA FORMA
Un efecto de las fuerzas es el cambio de forma de los cuerpos. Al estirar un muelle o al moldear plastilina, cambiamos la forma de esos cuerpos mediante fuerzas.
| ||||
Figura 9. Cuerpo elástico (bola de goma) y plástico (plastilina).
| Figura 10. Deformación de una bola de goma. |
Figura 11. Deformación de la plastilina.
| ||
Figura 12. Resultado de las deformaciones anteriores.
|
Figura 13. Cuerpo rígido. Roca de granito.
|
Figura 14. Cuerpo fragil. Vidrio.
| ||
Al estirar un muelle con una fuerza débil se deforma poco y tiende a recuperar la forma primitiva. Con una fuerza mayor es posible un cambio de forma permanente y, para fuerzas aún mayores, es probable que se llegue a la rotura.
9. LEY DE HOOKE
| Si de un muelle se cuelga un peso que realiza una fuerza F, se alarga una longitud l. Cuando se cuelga el doble de peso, el alargamiento es el doble. Si se cuelga el triple de peso, el alargamiento es el triple, etc. Este comportamiento lo resumió Robert Hooke en una ley que lleva su nombre: Ley de Hook. En los cambios elásticos la deformación es proporcional a la fuerza aplicada.
F = k . l
Donde F es la fuerza que actúa; k es la constante de elasticidad. Cuanto más grande sea k, más difícil será «estirar» el muelle. l0 es la longitud en reposo del muelle. Y l es la variación de longitud producida al actuar la fuerza.La longitud total será lf , de ahí: l = lf - l0 |
Supuesto práctico 2.
Un muelle tiene una constante de elasticidad de 100 N/m. Calcula qué deformación sufrirá cuando se fija en un extremo y se tira del otro con una fuerza de 10 N.
| A partir de la ley de Hooke: F = k · l Sustituyendo: 10 N = 100 N/m · l |



10. INTRODUCCIÓN A LA DINÁMICA
La cinemática describe el movimiento de los cuerpos usando conceptos como "sistema de referencia", "posición", "velocidad", "aceleración" etc;. Es decir, la cinemática estudia el movimiento de una forma cuantitativa, pero no se preocupa de las causas que lo producen.
La dinámica permite responder a preguntas como:¿Por qué un cuerpo tiene un determinado movimiento?¿Cómo podemos modificar la velocidad de un cuerpo?, etc. Para ello es necesario introducir nuevos conceptos como masa o fuerza.
Así como la cinemática está ligada al nombre de Galileo, la dinámica lo está al de Newton, quien, curiosamente, nació en el mismo año que murió Galileo (1.642).
La dinámica newtoniana se resume en tres leyes o principios acerca del movimiento, recogidos en su obra Principia Mathematica Philosophiae Naturalis.
Esta página está dedicada al estudio de dichos principios y de algunas de sus consecuencias. Hay que resaltar que el establecimiento de estos principios supuso un avance gigantesco en la ciencia física, hasta el punto que la dinámica newtoniana se desarrolló sin grandes cambios hasta principios del siglo XX
11. LAS FUERZAS CAMBIAN LA VELOCIDAD
| Siempre que veamos a un cuerpo cambiar su movimiento, debemos pensar en la acción de fuerzas. Cuando un coche acelera, frena o toma una curva lo hace gracias a fuerzas del motor, de los frenos, del volante, de los neumáticos sobre la carretera o de todas a la vez. Un efecto de la fuerza es la alteración del movimiento de los cuerpos Aplicando fuerzas podemos poner en movimiento un cuerpo que estaba en reposo; aumentar la velocidad de un cuerpo que ya estaba en movimiento; frenar o disminuir la velocidad de un cuerpo, incluso detenerlo; y hacerle cambiar la dirección en la que se movía. Definición: La dinámica es la parte de la física que estudia la relación entre las fuerzas y el movimiento de los cuerpos. Isaac Newton enunció las leyes que aún son la referencia. |
| Definición 1: Si sobre un cuerpo no actúan fuerzas o las que actúan se compensan, el cuerpo está en reposo o se mueve en línea recta con velocidad constante. DEFINICIÓN 2: Todo cuerpo permanece en su estado de reposo o movimiento rectilíneo y uniforme si no hay ninguna fuerza que lo saque de ese estado. |
ANIMACIONES
11.2. Segunda ley de Newton
Supuesto práctico 3
| Un muchacho, con calzado de clavos para no resbalar, empuja con una fuerza de 200 N a un compañero patinador de 45 kg de masa sobre una superficie helada que casi no presenta fricción. Luego hace lo mismo, con la misma fuerza, sobre otro compañero de 78 kg. ¿Tendrá los mismos efectos? Calcula la aceleración o aceleraciones que producirá a sus compañeros. Designemos como m1 la masa del primer patinador y m2 la del segundo. Del mismo modo serán a1 y a2 las aceleraciones que adquieran uno y otro. A partir de la segunda ley de Newton, en el primer caso:
|
Supuesto práctico 3
| Una nave espacial de 500 kg está parada en el espacio. Uno de sus cohetes la impulsa con una fuerza de 300 N durante 5 segundos. Calcula qué velocidad habrá adquirido al cabo de este tiempo. Para calcular la aceleración producida por el cohete, se aplica la segunda ley de Newton: La velocidad se calcula según la ecuación del m.r.u.a.:
La velocidad se calcula según la ecuación del m.r.u.a.:
vf = v0 + a • t ; vf = 0 + 0,6 m/s2 • 5 s = 3 m/s | Figura 23 |
Supuesto práctico 4
| Un coche de 450 kg que circula a 80 km/h frena hasta detenerse en 6 segundos. Calcula qué fuerza han realizado sus frenos. Primero, convertimos el valor de la velocidad a unidades del S.I.: Ahora, calculamos la aceleración necesaria para disminuir hasta 0 m/s en 6 s. Aplicamos la ecuación del m.r.u.a.:
De donde se halla: a = -3,7 m/s2
| Figura 24. | ||||
| La aceleración es negativa porque es un proceso de frenada. Obtenida la aceleración, ahora se obtiene la fuerza a partir de la segunda ley de Newton: Esta es la fuerza que deben ejercer los frenos del coche.
F = m • a
Sustituyendo: F = 450 kg • 3,7 m/s2 = 1 666, 7 NEsta es la fuerza que ejercen los frenos. ANIMACIONES       11.3. Tercera ley de Newton Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros. La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario. Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba. Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros. Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos. ANIMACIONES   12. FUERZAS DE ROZAMIENTO De mediciones experimentales se deduce que:
Ejemplo 1 De un cuerpo de masa 500 g se tira hacia la derecha, y paralelamente al plano, con una fuerza de 2 N. a) Calcular la aceleración con la que se mueve. b) ¿Cuál será su velocidad al cabo de 2,3 s si parte del reposo? Solución a) Diagrama de fuerzas actuantes: Eje Y : N – P = 0 ; N = P = m g Eje X: F = m a ; b) Como resultado de la acción de la fuerza F el cuerpo se mueve con aceleración constante igual a 4 m/s2. Por tanto estamos ante un movimiento uniformemente acelerado de ecuaciones: v = 0 + 4 t ; s = 0 + 0 + 2 t2 v (t = 2,3 )= 4 . 2,3 = 9,2 m/s
Ejemplo 2
Un cuerpo de m = 250 g es empujado hacia la derecha con una
fuerza de 1,5 N. Si el coeficiente de rozamiento entre el cuerpo y el plano es
de 0,4. Calcular:
a)
El valor de la fuerza de rozamiento.
b)
La aceleración con que se mueve.
c)
El
valor de la fuerza con que se debe empujar si se quiere que deslice con
velocidad constante de 1 m/s
Solución:
a)
Diagrama de
fuerzas actuantes:
Eje Y : N – P = 0 ; N
= P = m g
Cálculo de la fuerza de
rozamiento: F roz = m N = m m g = 0,4 . 0,250 kg . 10 m/s2
= 1 N
b)
Eje X : F – F roz = m a ;
c) Según la primera ley de Newton para que un cuerpo se
mueva con velocidad constante la resultante de todas las fuerzas que actúan
sobre él debe de ser nula:
La resultante de las que
actúan según el eje Y es nula ya que : :
N – P = 0
Para que sea nula la de las que actúan según el eje X
habrá de cumplirse: F – Froz = 0. Por tanto: F = Froz = 1 N. La fuerza deberá
equilibrar a la fuerza de rozamiento.
Para lograr que la
velocidad se mantenga invariable en 1 m/s se comunicaría esa velocidad al
cuerpo y entonces se haría F = 1 N.
Ejemplo 3
Un bloque de madera es lanzado con una velocidad de 4 m/s
por una superficie horizontal cuyo coeficiente de rozamiento vale 0,3.
a)
Describir el movimiento del bloque.
b)
Realizar
aquellos cálculos que permitan conocer los datos fundamentales del movimiento.
Solución:
a)
Diagrama de
fuerzas actuantes:
Como se observa la única
fuerza que actúa según el eje X es la de rozamiento. Como lleva sentido
contrario al de la velocidad va a comunicar al cuerpo una aceleración hacia la
izquierda. El cuerpo irá perdiendo velocidad hasta que se pare (movimiento
uniformemente decelerado)
b)
En este caso es
cómodo tomar como sentido positivo hacia la izquierda:
Froz
= m a;
m a = m N ; m a = m m g ; a = m g
Observar
que la aceleración (de frenada) no depende de la masa : a = 0,3. 10 m/s2
= 3 m/s2
Para calcular otros datos hacemos usos de las
ecuaciones de la cinemática. Como es un movimiento uniformemente acelerado
(decelerado):
v
= v0 + a t
En este caso v0 = 4 m/s; s0 = 0 ; a = - 3 m/s2
s
= s0 + v0 t + ½ a
t2
v = 4 – 3 t ; s = 4 t – 1,5 t2
Ecuaciones
del movimiento: v = 4 – 3 t ; s = 4 t –
1,5 t2
¿Cuánto
tiempo tardará en pararse?: 0 = 4 – 3 t
; t = 4 / 3 = 1,33 s
¿Qué
espacio recorre hasta que se para? s (t = 1,33 )= 4 . 1,33 – 1,5 .
1,332 = 2,67 m
ANIMACIONES13. PESO, LA FUERZA DEBIDA A LA GRAVEDAD
13.1. ¿Qué es la masa? | |||||
La masa es una propiedad fundamental de la materia. Todos los cuerpos materiales tienen masa, desde las partículas subatómicas hasta los planetas
La masa de un cuerpo no cambia si el cuerpo se rompe, cambia de forma, se dilata o se contrae. La masa es la propiedad de la materia que mejor nos permite cuantificarla.
DEFINICIÓN: La masa es la medida de la cantidad de materia que posee un cuerpo.
En el Sistema Internacional, la masa se mide en kilogramos (kg).
DEFINICIÓN: El kilogramo se define como la masa del kilogramo patrón, un cilindro fabricado con una aleación de platino e iridio, que se guarda en la Oficina Internacional de Pesos y Medidas en la localidad francesa de Sevres.
Los aparatos que usamos para medir masas son las balanzas que deben estar calibradas en kilogramos, gramos, miligrámos, etc.
13.2. ¿Qué es el peso?
| La atracción entre masas es una propiedad general de la materia. Así, la Tierra ejerce atracción sobre nosotros y los cuerpos situados en su superficie o proximidades.
DEFINICIÓN: Peso es la fuerza con que la Tierra atrae las masas situadas en su proximidad.
El peso es una fuerza y se expresa en newtons (N) en el S.l. El peso de un cuerpo se mide con unos aparatos llamados dinamómetros que estarán calibrados en newtons.Como se ha visto en la unidad anterior, si se deja caer libremente, un cuerpo cerca de la superficie terrestre caerá con una aceleración g = 9,8 m/s2. Esta es laaceleración de la gravedad terrestre. Si g es la aceleración de la fuerza de la gravedad terrestre, de acuerdo con la segunda ley de Newton (F = m • a )se tendrá que el peso de un cuerpo de masa m es:
Peso = m • g
La fuerza gravitatoria existe entre dos cuerpos cualesquiera del Universo, pero es muy débil y solo se nota cuando al menos uno de los cuerpos tiene una masamuy grande como ocurre con las estrellas y los planetas. Además es recíproca. O sea, el Sol atrae a la Tierra pero esta también atrae al Sol. En nuestro caso también podemos decir que del mismo modo que la Tierra nos atrae, nosotros atraemos a la Tierra. Ocurre que la masa de la Tierra es enorme comparada con la nuestra y así somos nosotros quienes «caemos» hacia ella y no al revés . |
| A diferencia de la masa, el peso no vale lo mismo independientemente de donde esté un cuerpo. Por ejemplo:
| Figura 26 . La gravedad terrestre tiene un valor g = 9,8 m/s2 a nivel del mar. En lo alto de una montaña su valor es menor y, si nos alejamos de la Tierra, sigue disminuyendo. |
| El peso como es una fuerza se mide con dinamómetros, que en realidad son muelles que se estiran al aplicarles una fuerza. Una variedad de un dinamómetro son las básculas que en realidad tienen muelles de los que se cuelgan masas y miden su peso, o sobre los que se ponen masas y miden, también sus pesos, como las básculas de baño. Supuesto práctico 6 Calcula el peso de un camión de 20000 kg y el de una motocicleta de 75 kg. A partir de la definición de peso: P = m • g, y del valor de la gravedad terrestre g = 9,8 m/s2: Para el camión: P = 20000 kg • 9,8 m/s2 = 196000 N Para la motocicleta: P = 75 kg • 9,8 m/s2 = 735 N |
Supuesto práctico 7
Calcula el peso de una persona de 60 kg de masa en la Tierra y en la Luna.
A partir de la definición de peso:
P = m • g
P = m • g
En la Tierra, g = 9,8 m/s2.
Sustituyendo: P = 60 kg • 9,8 m/s2 = 588 N
En la Luna, g = 1,6 m/s2.
| Si intentas empujar un balón lleno de aire dentro del agua, observarás la dificultad que conlleva. Dentro del agua, también habrás notado la sensación de «pesar» menos. Los fluidos (líquidos y gases) ejercen sobre los cuerpos sumergidos en ellos una fuerza que les empuja hacia la superficie del fluido. Aunque esto es más cotidiano en los líquidos también ocurre en los gases. Una prueba de ello es la fuerza ascensional que impulsa los globos aerostáticos. 14.1. Principio de ArquímedesLa fuerza que ejercen los fluidos sobre los cuerpos que se introducen en ellos depende de la densidad del fluido y del volumen sumergido del cuerpo, pero no depende de la forma, composición o densidad del cuerpo sumergido. El valor de esta fuerza ya fue estipulado por Arquímedes en su principio:
Principio de Arquímedes: Todo cuerpo sumergido total o parcialmente en un fluido, experimenta una fuerza ascensional igual al peso del volumen de fluido desplazado.
|
| El principio de Arquímedes se puede comprobar pesando con un dinamómetro un objeto sumergido, por ejemplo en agua, y también en el aire. En agua se obtendrá un peso (peso aparente) inferior al del objeto pesado en el aire. La diferencia entre los dos pesos es lafuerza ascensional del fluido. En un recipiente graduado, se mide el volumen del líquido antes de sumergir el objeto y el volumen aparente después de sumergido aquel. La diferencia entre ambos es el volumen desplazado. Se puede pesar este volumen desplazado de líquido y se comprobará que su peso es igual a la diferencia que marca el dinamómetro cuando pesa el objeto en el aire y cuando lo pesa sumergido. Si colocamos sobre agua (figura 65) distintos objetos: madera, plástico, papel, clavos, cubos de hielo, un barquito de papel, etc., veremos que algunos flotan y otros se hunden. Pero esto no depende únicamente del material, también depende de la forma que este tenga. Si con un mismo trozo de plasticina construyes una bola y un disco ahuecado, verás que el primero se hunde mientras que el segundo flota, según se ilustra en la figura 66. Por la misma razón un clavo de hierro se hunde y un barco, del mismo material, flota. Todas estas preguntas y los hechos señalados encuentran su explicación en el principio de Arquímedes. Ahora bien, lo interesante es comprender que el principio de Arquímedes es una consecuencia de la presión hidrostática. Para entender este punto sigamos el siguiente análisis ayudados por la figura 69. Allí se muestra un líquido de densidad D y sumergido en él un cuerpo cilíndrico de altura H y área A en su parte superior e inferior. En la superficie superior la presión es P1 = Dgh1, donde h1 es la profundidad a que se encuentra dicha superficie. Igualmente, en la superficie inferior es P2 = Dgh2. Arriba la fuerza producida por la presión actúa hacia abajo y la de abajo actúa hacia arriba, siendo mayor esta última dado que h2 > h1. F = F2 – F1; es decir, F = (P2 – P1)A, o bien, F = (Dgh2 – Dgh1)A; lo que se puede escribir como:
F = Dg(h2 – h1)A = DgHA;
Pero como el volumen del cilindro, y también el del líquido desalojado, es V = HA, encontramos que la fuerza que actúa hacia arriba y corresponde al empuje E es:
E = D . g . V
Como la masa del líquido desalojado es, m = DV, el empuje corresponde a E = mg, que es el peso del líquido desalojado. Así, hemos demostrado, gracias a las matemáticas, el principio de Arquímedes. No es muy difícil comprender que este es un resultado general; es decir, no depende de la forma del cuerpo que esté sumergido. 14.2. Empuje y peso aparente Todos hemos experimentado la sensación de sentirnos más livianos cuando estamos sumergidos en agua. Ello no se debe a una reducción de nuestro peso, sino a la presencia del empuje. Si haces el experimento que se ilustra en la figura 70, podrás constatar que en apariencia el peso de una piedra se reduce al sumergirla en agua. Por ejemplo, si al colgar la piedra del dinamómetro este indica que el peso de la piedra es de 10 newton (a) y al sumergirla en agua (b) indica 8 newton, ello se debe a que sobre la piedra, además de la fuerza de gravedad, está actuando el empuje que ejerce el agua. El peso de la piedra es 10 newton, su peso aparente 8 newton y el empuje 2 newton. Debes notar que, si consideramos que la densidad del agua es 1.000 kg/m3 y la aceleración de gravedad 10 m/s2, entonces, con la ecuación [6] podemos determinar el volumen de líquido desalojado y el de la piedra (que es el mismo). En efecto, por lo tanto: ANIMACIONES      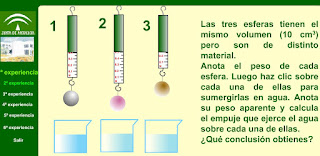  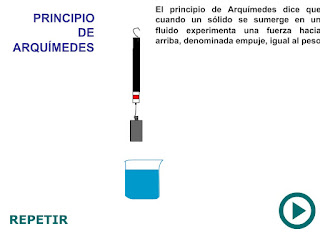 14.3. Flotabilidad
|
En esto se basa la flotabilidad de los barcos fabricados con materiales más densos que el agua pero que al tener grandes volúmenes vacíos desplazan gran cantidad de agua resultando de ello una gran fuerza ascensional.
|
Figura 30. Para que un barco flote, el peso desalojado del agua debe ser igual al peso del barco.
Sabemos que algunos objetos flotan sobre los líquidos y otros se hunden. Más exactamente, como lo indica la figura 71, hay tres posibilidades. Si el peso del objeto es mayor que el empuje (a), este se hunde hasta llegar al fondo del recipiente; si es igual al empuje (b), permanecerá “entre dos aguas”; y si es menor que el empuje (c), el cuerpo saldrá a flote y emergerá del líquido reduciéndose el empuje hasta hacerse igual al peso.
En la figura 72 se ilustra este último caso con más detalle. En (a) el cuerpo está completamente sumergido, pero como el empuje es mayor que su peso, está ascendiendo. Luego llegará a la posición que se indica en (b), pero igual que antes, seguirá ascendiendo. Desde este momento en adelante parte del cuerpo quedará por encima del nivel del líquido y el empuje se empezará a reducir, hasta hacerse igual a su peso. En este momento el cuerpo flotará en equilibrio. Las flechas azules indican el sentido del movimiento del cuerpo. En los líquidos en general, en tanto, las burbujas de aire u otros gases ascienden igual que un corcho, y lo hacen por la misma razón.
Problema 1:
En la figura 73 se ilustra un trozo de madera que flota en equilibrio sobre el agua. ¿Qué parte de él sobresale del agua?
Solución:
Si consideramos [1] tenemos que la masa del trozo de madera es: M = DV. Como la densidad de la madera es 0,42 g/cm3, tomando en cuenta las medidas dadas en la figura 73, tenemos que:
M = 0,42 g/cm3 · 10 cm · 10 cm · 8 cm
M = 336 g
Por lo tanto su peso es
Fg = mg = 0,336 kg · 10 m/s2 = 3,36 newton.
Esta fuerza debe ser igual al empuje que ejerce el agua, dado que la madera está en equilibrio. Luego, considerando [6] podemos escribir:
3,36 newton = 1.000 kg/m3 · 10 m/s2 · 0,10 cm · 0,10 cm · y
de donde y = 0,0336 m = 3,33 cm;
por lo tanto, como x + y = 8 cm, tenemos que
x = 4,64 cm.
Es importante advertir que el empuje no solamente actúa sobre cuerpos sumergidos en líquidos. En efecto, también actúa sobre los cuerpos sumergidos en la atmósfera. Por ejemplo, un globo lleno de helio, como el que sostiene la persona de la figura 74, asciende porque el empuje que el aire le aplica es mayor que su peso, siendo lo mismo lo que ocurre con los globos aerostáticos. Pero, por extraño que parezca, también actúa sobre las personas y todas las cosas que nos rodean. En otras palabras, cuando nos subimos a una pesa, ella marca un poco menos de lo que marcaría si la atmósfera no existiera. Por esta razón el procedimiento indicado en la figura 46 para determinar el “peso” del aire es incorrecto.
Hagamos una estimación del empuje que el aire le aplica a una persona. Si ella posee una masa de 60 kg y suponiendo que su densidad es igual a la del agua, tendremos que su volumen, considerando, es de 0,06 m3. Si la densidad del aire la consideramos igual a 1,29 kg/m3, entonces, el empuje que él ejerce sobre esta persona es del orden de 0,77 newton, que se puede despreciar si se lo compara con los 600 newton de su peso.
Ahora te mostraremos un juego entretenido. Introduce un gotario a medio llenar con agua en una botella plástica casi llena de agua, según se ilustra en la figura 75, y de modo que flote. Al cerrar la botella y presionar con los dedos sus paredes, podrás constatar que el gotario desciende y, al dejar de presionar la botella, asciende. Este juguete, conocido como ludión o diablillo de Descartes (pues a él se le atribuye su invención), se explica en base al principio de Arquímedes. ¿Cuál es esa explicación?
Para que este juguete funcione como lo hemos descrito y sea sensible a la débil presión que con las manos ejerzamos sobre los costados de la botella, es preciso ajustar el agua dentro del gotario de modo que, cuando flote sobre el agua, esté casi a punto de hundirse en ella.
14.4. La capilaridad y la tensión superficial
Al introducir diferentes objetos en agua u otros líquidos, observarás que las zonas en que dichos objetos están en contacto con la superficie de tales líquidos adoptan curvaturas especiales, que llamaremos meniscos. Si el objeto es un tubo capilar, inferior a unos 4 mm de diámetro interior, observarás que el nivel que alcanza el líquido dentro y fuera del tubo es diferente. También podrás constatar que algunos líquidos mojan de manera diferente los objetos; pero en algunos casos los líquidos no mojan en lo absoluto a los objetos, como es el caso del mercurio y el vidrio. En la figura 76 se ilustran los distintos efectos señalados hasta aquí.
Si bien estos efectos son pequeños y en la vida diaria suelen pasar desapercibidos, son de gran importancia y en muchos casos resultan de gran utilidad práctica. Estos fenómenos ocurren debido a que las moléculas de los distintos materiales interactúan eléctricamente con las moléculas de los líquidos y fluidos en general. Cuando el líquido moja al objeto, estas fuerzas son atractivas, y cuando no los mojan, repulsivas. Por otra parte, en las superficies de los líquidos estos átomos y moléculas se atraen entre sí más fuertemente que en otros lugares, produciendo lo que se denomina tensión superficial. El que los líquidos puedan ascender por delgados tubos se denomina capilaridad.
A continuación señalaremos distintas situaciones corrientes en que tales fenómenos tienen lugar. Es importante que realices las observaciones y experimentos que se proponen y te convenzas por ti mismo de lo que aquí se dice. Si calientas en un mechero un tubo capilar de vidrio y lo estiras cuando se esté fundiendo de modo que se adelgace lo más posible, observarás que al introducir un extremo en agua esta asciende varios centímetros por el tubo, como se indica en la figura 77. Prueba con capilares de diferentes diámetros; el efecto puede llegar a ser sorprendente. Si agregas al agua una gota de tinta china, posiblemente verás que el colorante no asciende por el tubo. ¿Por qué ocurrirá esto?
Hay papeles más absorbentes que otros. La publicidad de servilletas y toallas de papel suelen destacar esta propiedad. La figura 78 muestra el diseño de un experimento que permite evaluar este aspecto. Corta tiras de igual ancho pero de distintos papeles y cartones e introduce sus extremos en agua. Después de un rato verás que el agua asciende más en unos que en otros. ¿Qué fenómeno es el que está ocurriendo aquí? ¿Qué tienen los papeles que permiten que esto ocurra?
Con un alambre muy delgado construye un resorte cuyas espiras posean unos 2 cm de diámetro y midan unos 10 cm de largo cuando entre las espiras haya alrededor de 5 mm de distancia. En su extremo conforma una argolla lo más plana posible. Lo que has construido es un dinamómetro de gran sensibilidad, útil para poner en evidencia la tensión superficial en líquidos. Si introduces la argolla en agua, como se indica en la figura 79, constatarás que al levantar el resorte este se estira. Compara la tensión superficial que producen diferentes líquidos: aceite, mercurio, alcohol, etc.
Si eres muy cuidadoso y paciente, posiblemente serás capaz de poner una aguja de cocer sobre el agua sin que se hunda (figura 79). Si no tienes tanta paciencia, puedes lograrlo pasando primero la aguja por una vela (parafina sólida). ¿Qué efecto producirá la esperma?
Posiblemente has visto que algunos insectos pueden caminar sobre el agua, ¿cómo lo lograrán? Dato curioso: si una piscina estuviera llena de mercurio en vez de agua, podrías caminar por su superficie al igual que algunos insectos en el agua.
Si disuelves un poco de jabón en agua e introduces en ella una argolla, al sacarla podrás ver una delgada película de líquido que se sostiene en los bordes de la argolla. Si soplas suavemente podrás formar hermosas burbujas que vuelan por el aire hasta reventar en el momento de tocar un objeto. Al agitar la superficie del agua jabonosa también podrás ver que en ella se forman numerosas burbujas. ¿Cómo explicas la formación de las burbujas?
15. CANTIDAD DE MOVIMIENTO
La cantidad de movimiento o momento lineal,p, de un objeto en movimiento se define como:
P es un vector que tiene la misma dirección de v
Combina dos magnitudes que intervienen en el cambio de movimiento que produce la fuerza: la masa, que refleja la tendencia del cuerpo a permanecer como está (inercia), y la velocidad.
Se define incremento de cantidad de movimiento como: Dp = m·Dv
El Impulso mecánico (I = F · t) equivale al incremento de p, Dp. Es decir, una fuerza actuando un tiempo t sobre un objeto origina un incremento en su cantidad de movimiento: F· t = m· Dv
La cantidad de movimiento o momento lineal
La unidad de cantidad de movimiento en el S.I. es el kg·m/s , que no tiene nombre propio.
15.1. Conservación de la cantidad de movimiento
Principio de Conservación: En ausencia de fuerzas externas la suma de la cantidad de movimiento de los cuerpos que interviene en un choque no varía(Pantes= Pdespués)
Si dos partículas de masa mA y mB que se mueven conVA y VB chocan, sus masas se conservan igual y su cantidad de movimiento total también.
Pantes= mAVA+ mBVB ; Pdespués= mAV´A+ mBV´B
Pantes= Pdespués;
mAVA + mBVB= mAV´A+ mBV´B
mAVA-mAV´A= - (mBVB- mBV´B ); Fórmula (I)
La variación de cantidad de movimiento de A es:
DpA= mAVA- mAV´A
Sustituyendo en la fórmula(I);
nDpA= - DpB
|
16. PRÁCTICAS
| Relaciona Asocia Completa el texto Autoevaluación Problemas 1 Ejercicios resueltos Ejercicios resueltos 2 Cuaderno de ejercicios Cuadernillo actividades Ejercicios 1 Soluciones Ejercicios 2 Ejercicios 3 Ejercicios 4 Ejercicios 5 Ejercicios 6 Ejercicios 7 Ejercicios 8 |
Cuestiones
Las interacciones fundamentalesComposición de fuerzas Calcular la fuerza Ejercicios de operaciones con vectores Ejercicios de equilibrio de fuerzas Ejercicios Leyes de Newton Ejercicios de Impulso y cantidad de movimiento Fuerzas y presiones Asocia Verdadero o falso Fuerzas y equilibrio. Fuerzas y materiales. Fuerza y movimiento. Fuerza gravitatoria. Dinámica Jclic |
18. VÍDEOS
2ª Ley de Newton
| ||
Acción-reacción
|
Efectos de las fuerzas
|
Fuerza de rozamiento
|
La ley de Newton (Universo mecánico)
|





























































No hay comentarios:
Publicar un comentario