ÍNDICE
|
10. Movimiento rectilíneo uniforme
11. Aceleración
1. Aceleración y frenado
12. Movimiento rectilíneo uniformemente acelerado
13. La aceleración de la gravedad
14. Movimiento circular uniforme
1. La aceleración centrípeta
15. Movimiento circular uniformemente acelerado
17. Tiro parabólico16. Movimientos compuestos
18. Lanzamiento en la vertical
19. Tiro horizontal
20. Resumen
31. Prácticas
22. Cuestiones
23. Vídeos
|
1. ESQUEMAS
2. PRESENTACIONES



3. CONTENIDOS ANIMADOS





4. DEFINICIONES
MAGNITUD: Es todo aquello que se puede medir. Ejemplos: superficie, presión, fuerza, etc.
MAGNITUDES FUNDAMENTALES: Son aquellas a partir de las cuales se pueden deducir todas las demás. En mecánica las magnitudes fundamentales son: longitud, masa y tiempo.
UNIDADES PATRÓN: Son : de longitud : el metro (m) , de masa : el kilogramo (kg) y de tiempo : el segundo (s).
MAGNITUDES DERIVADAS: Son aquellas que se pueden expresar en función de las magnitudes fundamentales. Ejemplo: la velocidad. v = e / t
MAGNITUDES ESCALARES Y VECTORIALES.
- Magnitudes escalares. Son aquellas que quedan definidas por el valor de su medida. Ejemplos: la masa y el tiempo.
- Magnitudes vectoriales. Son aquellas que para definirlas es necesario conocer, además de su medida, su dirección y sentido. Se representan mediante vectores. Ejemplos: la fuerza y la velocidad.
VECTOR: Es un segmento orientado. En Física utilizaremos a los vectores para representar magnitudes vectoriales (velocidad, posición, aceleración, fuerza, …) o
Partes de un vector :
- Módulo. Es la longitud del vector.
- Dirección. Es la recta sobre la cual se encuentra
- Sentido. Es el que indica la punta de flecha.
- Origen o punto de aplicación. Es el origen del vector. Los vectores se representan de la siguiente forma:
CINEMÁTICA: Es la parte de la Física que estudia los movimientos de los cuerpos sin tener en cuenta las causas que los producen. El objetivo de la cinemática es conocer en cualquier instante la posición r(t) , la velocidad v(t) y la aceleración a(t) del móvil.
MOVIMIENTO: Se dice que un cuerpo se mueve cuando cambia de posición respecto a un punto de referencia. Se llama movimiento absoluto si el punto de referencia es fijo y movimiento relativo si el punto de referencia es móvil. Como en el Universo no existe ningún punto fijo de referencia, todo movimiento es relativo.
TRAYECTORIA: Es el conjunto de puntos por los cuales pasa un móvil al desplazarse. Si los móviles dejasen rastro por donde van pasando, la trayectoria sería la línea que describirían. Existen trayectorias muy sencillas (rectilínea o circular), pero las hay más complejas (parabólicas, elípticas, hiperbólicas), o extremadamente complejas entre las curvilíneas (vuelo de una mosca, movimiento de la mano de un saltador de trampolín).
POSICIÓN DE UN MÓVIL: Para determinar la posición de un móvil se pueden tomar unos ejes coordenados de referencia. Si el móvil se mueve en un plano se puede localizar éste mediante su abscisa y su ordenada en cada instante.
Otras veces resulta más cómodo medir las posiciones sobre la propia trayectoria. Para fijar una posición medida sobre la trayectoria es necesario fijar un punto O, al que asignaremos la posición cero; este punto es el denominado origen.
VECTOR DESPLAZAMIENTO: Para un móvil que parte de un punto A y llega a otro B se llama vector desplazamiento al vector que tiene como origen el punto A y como extremo el punto B.


VELOCIDAD MEDIA: Es el cociente entre el espacio total recorrido por un móvil y el tiempo empleado en recorrerlo.
UNIDAD DE VELOCIDAD: En el S.I. (Sistema Internacional) es : m/s
VELOCIDAD INSTANTÁNEA: Es el cociente entre el espacio recorrido por un móvil entre dos puntos muy próximos y el tiempo (un instante) empleado en recorrerlo.
CARÁCTER VECTORIAL DE LA VELOCIDAD: La velocidad es una magnitud VECTORIAL, es decir la podemos representar mediante un vector. La velocidad de un móvil en cada punto de su trayectoria es un vector cuyo módulo es el valor de la velocidad instantánea en el punto; la dirección es la tangente en el punto a la trayectoria y el sentido el del movimiento del móvil.
- Si un móvil tiene rectilínea su dirección no cambia, y el vector velocidad no cambia de dirección.
- Si la trayectoria es rectilínea y el móvil se da la vuelta (avanza y de repente retrocede), el vector velocidad cambia también de sentido, pero no de dirección. Cualquier trayectoria no rectilínea supone cambios continuos del vector velocidad. (Ejemplo: movimiento circular uniforme)
ACELERACIÓN: La aceleración es una magnitud que nos mide cómo cambia la velocidad de un móvil. Recuerda que la velocidad puede cambiar:
1. Sólo de módulo, y nos originará una aceleración tangencial
2. Sólo de dirección, y nos originará una aceleración normal
3. De dirección y de módulo, y nos originará aceleración tangencial y normal.
- En los movimientos rectilíneos, sólo tendremos aceleración tangencial ya que el vector velocidad no varía su dirección y por lo tanto no tendremos aceleración normal.
- En los movimientos circulares uniformes (a velocidad –módulo- constante) no tendremos aceleración tangencial y sólo tendremos aceleración normal.
- En los movimientos curvilíneos no uniformes tendremos de las dos.
ACELERACIÓN TANGENCIAL MEDIA: Es el cociente existente entre la variación del módulo de la velocidad y el tiempo invertido en producir esa variación.
ACELERACIÓN NORMAL: Es la aceleración que posee un móvil debido al cambio de dirección del vector velocidad. Un móvil que se desplaza siguiendo una trayectoria circular con velocidad constante v tiene una aceleración normal que viene dada por la expresión:
donde v es el módulo de la velocidad, y r el radio de la trayectoria.
- En los movimientos circulares, r es el radio de la circunferencia.
- En otros movimientos curvilíneos el radio de la trayectoria varía.
- En los movimientos rectilíneos, r es ∞ y an=0
MAGNITUDES ANGULARES. RADIAN
Es un ángulo cuyo arco S correspondiente rectificado tiene la misma longitud que el radio con el que ha sido trazado.
Es un ángulo cuyo arco S correspondiente rectificado tiene la misma longitud que el radio con el que ha sido trazado.
En otras palabras, el arco es igual al ángulo (rad) por el radio:
El número de radianes de un ángulo se obtiene dividiendo la longitud del arco correspondiente entre el radio con el que ha sido trazado.
Si llamamos ∆S al arco recorrido e ∆φ al ángulo barrido por el radio:
 El radian (unidad de medida en el SI) es el ángulo cuya longitud del arco es igual al radio.
El radian (unidad de medida en el SI) es el ángulo cuya longitud del arco es igual al radio.
Si llamamos ∆S al arco recorrido e ∆φ al ángulo barrido por el radio:
Es importante señalar que es adimensional ya que es el cociente de dos longitudes. El radián por tanto no es una unidad.
NÚMERO DE RADIANES DE UNA CIRCUNFERENCIA: Teniendo en cuenta que la longitud de una circunferencia es 2 r , el número de radianes de ésta será :
VELOCIDAD ANGULAR: Para un móvil que describe una trayectoria circular se define la velocidad angular como el cociente que existe entre el ángulo descrito por el móvil y el tiempo empleado en describirlo.
UNIDADES DE VELOCIDAD ANGULAR: En el S . I . es rad/s. Frecuentemente se utiliza como unidad de velocidad angular la revolución por minuto
RELACIÓN ENTRE LA VELOCIDAD LINEAL Y LA ANGULAR. La velocidad lineal es igual a la velocidad angular multiplicada por el radio.
Atendiendo a la trayectoria, los movimientos se clasifican en :
- Rectilíneos. Si la trayectoria es una línea recta. A B
- Curvilíneos. Si la trayectoria es una línea curva. B A A
Atendiendo a la velocidad, los movimientos pueden ser :
- Uniformes . Si el valor de la velocidad es constante. A B C D vA = 5 m/s vB = 5 m/s vC = 5 m/s vD = 5 m/s
- Uniformemente variados o uniformemente acelerados. Si tienen aceleración tangencial constante.
MOVIMIENTO RECTILÍNEO Y UNIFORME (MRU)
CAÍDA LIBRE DE LOS CUERPOS
MOVIMIENTO CIRCULAR UNIFORME
El movimiento es un fenómeno cotidiano. Tan cotidiano que es imposible encontrar algún objeto o sistema material que no se mueva, por lo tanto para definir uel movimiento de un cuerpo tenemos que fijar otro cuerpo o sistema marial que consideramos fijo, al que llamarémos sistema de referencia. Una vez definido este sistema de referencia para estudiar científicamente el movimiento de un cuerpo respecto a este sistema de referencia hay que conocer los distintos lugares por los que va pasando un cuerpo y el tiempo que tarda en ir de uno a otro.
La parte de la física que estudia el movimiento de los cuerpos se conoce como cinemática.
Figura 1-bis. En el universo toda la materia está en movimiento.
Los cuerpos materiales «ocupan» un lugar en el Universo. Y el lugar que ocupan, no puede ser ocupado por otros cuerpos. El lugar que ocupa algo o alguien es lo que conocemos por su posición. Posición es el lugar que un cuerpo ocupa en el espacio respecto al sistema de referencia que consideramos como inmovil. . Para indicar dónde estamos o están las cosas, damos referencias a algo conocido y distancias entre la referencia y lo que se va a localizar. Decimos: «mi casa está a 40 m del colegio », «estoy a 22 km de Guadalajara » o «el Sol está a 150 000 000 km de la Tierra»: Dar una posición es dar una referencia a algo conocido (sistema o punto de referencia) y una distancia a ella. Ejemplos de sistema de referencia: El punto cero de las carreteras españolas está en la Puerta del Sol de Madrid; La altura a la que vuela un avión se cuenta a partir del nivel del mar en Alicante, La longitud terrestre se cuenta a partir del meridiano de Greenwich. Para indicar la posición de los objetos, los científicos usan los sistemas de referenia. El más conocido es el llamado cartesiano (ejes cartesianos) en honor a Rene Descartes, matemático francés del siglo XVIII. Consta de tres rectas llamadas ejes de coordenadas que se cortan en ángulos de 90° en un punto llamado origen. Cada eje está graduado en unidades de medida y acostumbran a designarse con las letras x, y, z. |
ANIMACIONES


6. POSICIÓN DE UN PUNTO
Es muy común que representemos un vector utilizando los valores de sus componentes.
Las componentes cartesianas de un vector son los vectores que se obtienen al proyectarlo sobre los ejes de un sistema de coordenadas situado en el origen del vector.
El siguiente simulador dibuja automáticamente las componentes del vector A. Puedes pulsar y arrastrar con el ratón el extremo del vector.
Cuando hayas practicado un poco, prueba a representar los siguientes vectores:
|
|
Observa que la suma vectorial de ambas componentes da como resultante nuestro vector A, dibujado en gris en el simulador.
También podemos representar un vector a través de sus componentes polares. Si quieres saber sobre esto puedes visitar las páginas sobre la posición y el vector de posición.
ANIMACIONES



| Relación entre las componentes cartesianas y polares Aprende cómo se calculan las componentes cartesianas a partir de las polares y viceversa. | Resta de vectores Aprende a restar vectores de forma gráfica y analítica. | ||
| Suma de vectores Regla del paralelogramo para sumar vectores. Componentes expresadas como (x, y) | Suma de vectores I Regla del paralelogramo para sumar vectores. Los vectores se expresan como suma de sus componentes x e y. | ||
| Suma de vectores II Aprende a sumar vectores de diferentes formas. | Suma gráfica de vectores Aprende a sumar varios vectores gráficamente. |
6.1. Vector de Posición
Si ya sabes cómo se determina la posición de un punto, es muy fácil entender qué es un vector de posición.
Construye una definición para el vector de posición y muéstrasela a tu profesor para conocer su opinión sobre la misma.
7. LAS UNIDADES DE MEDIDA
En el Sistema Internacional la unidad de medida para las distancias (longitud) es el metro. Pero no siempre es la unidad más apropiada.
Para cuerpos como estrellas o galaxias, las medidas y distancias a las que están son tan grandes que el metro es poco práctico y se usa el año luz, que es la distancia que la luz recorre en un año en el vacío.
En el mundo de los átomos o de las moléculas, las distancias son tan pequeñas que se recurre a unidades submúltiplos del metro. Corrientemente se usan micrómetros o nanómetros para estos fines. En la Tabla 1.1 se recuerdan algunas unidades.
Según las dimensiones de los objetos y las distancias se habla de:
- Observación microscópica, si los objetos son de tamaño que escapa a la visión humana. Así, los átomos, moléculas, virus, células y tejidos animales o vegetales deben observarse con microscopios y otros instrumentos.
- Observación macroscópica, si los objetos se observan a simple vista. Por ejemplo, la de nuestros objetos cotidianos o de la geografía terrestre.
- Observación astronómica, si se observan objetos muy lejanos (fuera de la Tierra) a distancias muy superiores a las de la escala humana y terrestre.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8. ¿QUÉ ENTENDEMOS POR MOVIMIENTO?Todos tenemos claro cuándo algo se mueve y cuándo está quieto. Aunque a veces las cosas se mueven tan lentamente que parecen quietas y otras veces tan rápido que ni las vemos. Una definición sencilla de movimiento es:Definición: Un cuerpo se mueve cuando cambia de posición respecto a un sistema de referencia que consideramos fijo. Un cuerpo no pasa de una posición a otra de repente sino a través de una serie de posiciones intermedias. Hay un camino que sigue un cuerpo al moverse. Definición: Trayectoria es la línea que resulta de unir todos los puntos correspondientes a las sucesivas posiciones de un móvil. La trayectoria comienza en el punto de salida u origen y acaba en el punto de llegada o final. Aunque las trayectorias para moverse un punto de origen y un punto final pueden ser muchas, infinitas. Por ejemplo, para ir de Macrid a Sevilla, se puede ir por distintas carreteras y pasar por diferentes ciudades. Recuerda. Móvil es cualquier cuerpo que se mueve. Cinemática es el estudio del movimiento (del griego kinetos, movimiento). Según su trayectoria los movimientos se clasifican en:
| |
Figura 6. Movimiento rectilíneo | Figura 7. Movimiento curvilíneo. Parabólico. |
Figura 8. Movimiento curvilíneo. Elíptico. | Figura 9. Movimiento curvilíneo. Circular. |
8.1. Recorrido y desplazamiento
Supongamos un piloto de Formula 1 sale del "Pitlane" para correr una carrrera en circuito de 5 073 metros al que tiene que dar 61 vueltas, cuando acaba la carrera vuelve al "box" de su equipo y deja el coche en el mismo sitio del que partió. Nadie podrá negar que el automóvil ha «recorrido» un buen número de kilómetros, 309,45 km exactamente, pero, ¿cuál ha sido su «desplazamiento»?
Hay dos conceptos diferentes:
Recorrido es la longitud de la trayectoria de un móvil.
Definición: Distancia recorrida (s) es la longitud de la trayectoria descrita por el móvil desde su posición inicial, xi, hasta la final, xf.
Hay dos conceptos diferentes:
Recorrido es la longitud de la trayectoria de un móvil.
Definición: Distancia recorrida (s) es la longitud de la trayectoria descrita por el móvil desde su posición inicial, xi, hasta la final, xf.
s = xf – xi
Desplazamiento es la distancia (en línea recta) entre el punto origen y el punto final.
Definición. Desplazamiento es la diferencia entre las posiciones inicial y final del móvil, pero medida en línea recta.
En el caso de del piloto de formula 1 el la trayectoria es el recorrido del circuito, la distancia recorrida es lo que mide el circuito multiplicado por el nº de vueltas..... pero el desplazamiento es CERO, la posición inicial y la posisción final cinciden n el mismo punto.
Figura 10. Circuito de carreras Figura 11. Relación entre trayectoria, distancia recorrida y desplazamiento
8.2. Movimiento absoluto y relativo
| Si varias personas viajan juntas en un mismo autobus, para alguien que mire desde la acera se están moviendo todos ocupantes del autobus. En cambio, para cada uno de los ocupantes que estan sentados los otros ocupantes sentados a estan quietos. | Otro ejemplo: alguien corre dentro de un vagón de tren con igual velocidad que el tren pero en sentido contrario. A los ocupantes del vagón les parece que el individuo se mueve hacia atrás pero a un observador desde el andén le parece que el tren se mueve pero el individuo que está corriendo no se mueve respecto al andén. |
Figura 12. | Figura 13. |
En general, según el sistema de referencia que se escoja, se designa como:
- Movimiento absoluto, cuando se mide el movimiento respecto a un sistema de referencia que está "quieto". Por ejemplo, si estudiamos el movimiento de los corredores de cien metros lisos respecto a la línea de salida.
- Movimiento relativo, cuando se mide el movimiento respecto a un sistema de referencia que no está fijo. En el mismo ejemplo anterior, se puede estudiar el movimiento relativo de un corredor respecto a otro a lo largo de la carrera.
9. ¿QUÉ ES LA VELOCIDAD?
Llamamos veloces a las cosas que cambian mucho su posición en poco tiempo, mientras que llamamos lentas a las que tardan mucho en cambiar de posición.9.1. El concepto de velocidad
Este concepto intuitivo de rapidez o lentitud de movimiento se corresponde con una magnitud física que conocemos como velocidad.
Para estudiar el cambio de posición o movimiento de un cuerpo se necesita:
Un sistema de referencia para medir cambios de posición de un cuerpo.
Una medida de tiempo que indique lo que tarda en cambiar de posición.
Físicamente, la velocidad, v, se define como la distancia recorrida, s, dividida por el tiempo, t, que el móvil ha tardado en recorrerla.

Para saber cómo se mueve un cuerpo no basta con dar el valor de su velocidad. Se debe indicar también en qué dirección se mueve y hacia dónde, "sentido". Así, si decimos que un coche se mueve a 80 km/h la información es incompleta ya que puede moverse hacia muchos sitios.
En países anglosajones aún se usan las millas por hora (1 mph = 1,6093 km/h). Los vehículos náuticos acostumbran a medir la velocidad en nudos que equivalen a millas náuticas por hora (1 nudo= 1,852 km/h).
Supuesto práctico 1
Un motorista circula durante media hora recorriendo 45 kilómetros . Calcula su velocidad en metros por segundo.
Se pasa el tiempo a segundos:

A partir de la definición de velocidad

A partir de la definición de velocidad:

9.2. La velocidad instantánea y la velocidad media
Se debe distinguir entre dos conceptos de velocidad:- La velocidad instantánea es la que tiene un móvil en un determinado instante de tiempo, en el momento en que se mide.
- La velocidad media es la velocidad obtenida al dividir el recorrido total por el tiempo total empleado.
Un motorista circula durante media hora a una velocidad de v 1 = 40 km/h. El cuarto de hora siguiente lo hace a v2 = 50 km/h. Finalmente, pasa 1 hora circulando a v3 = 70 km/h. Calcula su velocidad media.
El tiempo total que ha estado circulando es de:
t t = t 1 + t2 + t 3 = 0,5 h + 0,25 h + 1 h = 1,75 h
El espacio recorrido total es la suma de los espacios recorridos en los intervalos :

El espacio total recorrido será:
st = s1 + s2 + s3 = 20 km + 12,5 km + 70 km = 102,5 km
El tiempo total empleado es:
t t = t 1 + t2 + t 3 = 0,5 h + 0,25 h + 1 h = 1,75 h
Con ello, la velocidad media será:

| |||||
Velocidades de máquinas y fenómenos físicos | Velocidades de seres vivos |
Figura 16. | Figura 17. |
| Velocidades máximas alcanzadas por algunos seres vivos y por maquinas y el sonido. | |
10. MOVIMIENTO RECTILÍNEO Y UNIFORME
El movimiento rectilíneo uniforme es el más simple y fácil de estudiar. Las características que le definen son:Movimiento rectilíneo. El cuerpo se mueve sobre una línea recta.
Movimiento uniforme. La velocidad del móvil no varía, es constante.
Un cuerpo se mueve con un movimiento rectilíneo y uniforme (m.r.u.) si se mueve siguiendo una trayectoria recta con una velocidad constante, eso quiere decir que recorre espacios iguales en tiempos iguales . La ecuación fundamental del m.r.u. es la misma ecuación de la velocidad:

t = tiempo empledo
v = velocidad
En la Figura siguiente se muestra un móvil con un m.r.u. indicando las posiciones que ocupa y el tiempo que tarda en llegar a ellas desde la salida.
Figura 18. En un m.r.u. el móvil recorre los mismos espacios en los mismos tiempos. |
La Figura 18 representa la posición del automóvil en cuatro instantes:
- Al comenzar a contar el tiempo (t = 0 s) el coche está en el origen (s = 0 m).
- En 15 segundos (t = 15 s) el coche recorre 500 m y llega a la posición s = 500 m.
- En los siguientes 15 segundos (cuando t = 30 s) el coche recorre 500 m más y llega al punto s = 1 000 m.
- Y, al cabo de 15 segundos más (cuando t = 45 s), el automóvil ha vuelto a recorrer 500 m más y ha llegado al pnto s = 1 500 m.
| t | 15 s | 30 s | 45 s |
| s | 500 m | 1 000 m | 1 500m |
Tabla 2. La tabla muestra cómo en tiempos iguales, el móvil recorre espacios iguales y su velocidad no varía.
10.1. La representación gráfica del m.r.u.
Para representar gráficamente el m. r. u. se utilizan los ejes de coordenadas x e y.- En el eje x se representa el valor del tiempo (t).
- En el eje y se representa el valor del espacio (s).
También se puede representar la velocidad en función del tiempo, tomando pares de valores velocidad - tiempo (v, t). Se representa la "v" en el eje "y" y el tiempo el eje x. Como la velocidad siempre es la misma, la representación resulta una recta paralela al eje de las x. Estudia el siguiente supuesto práctico
Supuesto práctico 3
Un ciclista circula por una carretera reta cinco mnutos a una velocidad constante de 30 km/h. Calcula el espacio recorrido y dibuja las gráficas del espacio y de la velocidad respecto al tiempo.
Primero se pasan la velocidad y el tiempo a unidades del sistema internacional:


El espacio recorrido, al tratarse de un movimiento rectilíneo y uniforme, se hallará a partir de: s = v · t
Por tanto, el espacio total será:
s = 8,33 m/s · 300 s = 2500 m
.Se puede calcular la tabla de valores para la velocidad y el espacio al cabo de distintos valores del tiempo. Pongamos que se calcula para el momento inicial (t = 0) y para cada uno de los cinco primeros minutos:
Para el momento inicial (t = 0 s) es: s = v · t = 8,33 m/s · 0 s = 0 m
Para el primer minuto, t = 60 s, es: s = v · t = 8,33 m/s · 60 s = 500 m
Para el segundo minuto, t = 120 s, es: s = v · t = 8,33 m/s · 120 s = 1000 m
Y así sucesivamente. Los valores de v (que es siempre la misma) y s recogidos en la Tabla 1.3 son:
| 0 | 60 | 120 | 180 | 240 | 300 | |
| v(m/s) | 8,33 | 8,33 | 8,33 | 8,33 | 8,33 | 8,33 |
| s(m) | 0 | 500 | 1 000 | 1 500 | 2 000 | 2 500 |
- La gráfica del espacio respecto al tiempo es una recta. Pasa por el origen porque en el momento inicial (t = 0) el móvil todavía no ha recorrido ningún espacio (s = 0)
- La gráfica de la velocidad es una línea paralela al eje del tiempo porque el valor de la v es 8,33 m/s invariablemente cualquiera que sea el valor del tiempo.





















11. ¿QUÉ ES LA ACELERACIÓN?
Aceleración es una palabra conocida. Cuando un automóvil aumenta su velocidad decimos que acelera (el propio pedal del automóvil recibe el nombre de acelerador). Un móvil acelera siempre que cambia de velocidad y su aceleración es mayor cuanto mayor es el cambio y menor el tiempo empleado.
Definición: Aceleración es la rapidez con que los cuerpos cambian de velocidad.
Cuando alguien o algo que estaba en reposo empieza a moverse, acelera porque pasa de velocidad cero a una velocidad distinta de cero.
Cuando un móvil disminuye su velocidad sufre una aceleración negativa. De ordinario decimos que frena.
Si un móvil que pasa de una velocidad inicial, vi, a una velocidad final, vf,. Esto lo realiza en un tiempo t. Durante este tiempo, el móvil se mueve de la posición inicial, si, a la posición final, sf.
La aceleración se define como la diferencia entre la velocidad final y la velocidad inicial, vf - vi, dividida por el tiempo t que tarda en realizar este cambio de velocidad:


La aceleración es una magnitud física que en el S. I. se mide en metros por segundo al cuadrado (m/s2).Definición: Aceleración es la rapidez con que los cuerpos cambian de velocidad.
Cuando alguien o algo que estaba en reposo empieza a moverse, acelera porque pasa de velocidad cero a una velocidad distinta de cero.
Cuando un móvil disminuye su velocidad sufre una aceleración negativa. De ordinario decimos que frena.
Si un móvil que pasa de una velocidad inicial, vi, a una velocidad final, vf,. Esto lo realiza en un tiempo t. Durante este tiempo, el móvil se mueve de la posición inicial, si, a la posición final, sf.
La aceleración se define como la diferencia entre la velocidad final y la velocidad inicial, vf - vi, dividida por el tiempo t que tarda en realizar este cambio de velocidad:


La velocidad, por su carácter de vector, tiene módulo (rapidez), dirección y sentido. La aceleración también es un vector y según qué aspecto de la velocidad modifica recibe un nombre distinto.
- Aceleración tangencial, modifica la rapidez del movimiento. (módulo de la velocidad).
- Aceleración normal, modifica la dirección del movimiento (dirección de la velocidad).
Si la aceleración tangencial es constante a lo largo de todo un recorrido, la gráfica que refleja los valores de la velocidad a cada instante es una línea recta.
La velocidad media en un m.r.u.a. será:

Un automóvil pasa de 6 m/s a 10 m/s en un tiempo de 5 segundos. Calcula su aceleración.
El cambio de velocidad es: vf - vi = 10 m/s - 6 m/s = 4 m/s
El enunciado indica que el tiempo empleado es de 5 s. Así. la aceleración será:

Observa que, al tratarse de metros por segundo, m/s, divididos por segundos, s, las unidades son metros por segundo al cuadrado, m/s2.
ANIMACIONES
11.1. La aceleración y deceleración o frenado
En nuestra vida cotidiana decimos que aceleramos cuando aumentamos la velocidad y decimos que frenamos cuando disminuimos la velocidad. En realidad, tan cambio de velocidad es un aumento como una disminución. En ambos casos hay una .aceleración Díferenciamos entre:
Supuesto práctico 5
Un automóvil pasa de 4 m/s a 8 m/s en un tiempo de 2 segundos. Calcula su aceleración. Calcula también la aceleración para retornara la velocidad inicial en el mismo tiempo de 2 segundos.
El incremento de velocidad es: vf - vi = 8 m/s - 4 m/s = 4 m/s
El tiempo, r, es de 2 s. Así, la aceleración será:
 En la segunda parte del problema, cuando el automóvil retorna a la velocidad inicial, pasa de 8 m/s a 4 m/s en un tiempo también de 2 segundos:
En la segunda parte del problema, cuando el automóvil retorna a la velocidad inicial, pasa de 8 m/s a 4 m/s en un tiempo también de 2 segundos:
La variación de velocidad es: vf - vi = 4 m/s - 8 m/s = - 4 m/s
El tiempo, t, para este cambio es de 2 s. Así, la aceleración será:
 Los valores de las aceleraciones son los mismos pero sus signos son distintos. En el primer caso la aceleración actúa aumentando la velocidad y en el segundo, disminuyéndola.
Los valores de las aceleraciones son los mismos pero sus signos son distintos. En el primer caso la aceleración actúa aumentando la velocidad y en el segundo, disminuyéndola.
12. MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO
El movimiento rectilíneo y uniformemente acelerado, m. r. u. a., se caracteriza por ser:
Para saber qué velocidad final, vf , alcanzará a partir de una velocidad inicial, vi , cuando actúe una aceleración, a, durante un tiempo, t, se usa la siguiente igualdad:
vf = velocidad final
vi = velocidad inicial
a = aceleración
t = tiempo
La igualdad anterior se obtiene de la definición de aceleración, despejando:
 El espacio recorrido, s, durante un movimiento uniformemente acelerado, se calcula a partir de la siguiente igualdad:
El espacio recorrido, s, durante un movimiento uniformemente acelerado, se calcula a partir de la siguiente igualdad:
 s = espacio recorrido
s = espacio recorrido
v = velocidad inicial
a = aceleración
t = tiempo
Dado que en un MRUA la velocidad varía con el tiempo, para describirlo necesitaremos, además de la posición xi, la velocidad vi en el instante inicial y la aceleración a que actúa sobre el móvil.
Si partimos de la definición de aceleración media:
 tomando de nuevo ti=0 y como en un MRUA la aceleración permanece constante:
tomando de nuevo ti=0 y como en un MRUA la aceleración permanece constante:
 que es la ecuación de la velocidad en un MRUA.
que es la ecuación de la velocidad en un MRUA.
Para obtener la ecuación de la posición, podemos aprovecharnos del hecho que la velocidad media es constante en el cualquier intervalo, dado que la aceleración es constante. Entonces:



Un motorista circula a 4 m/s y acelera durante 2 s con una aceleración de 1,5 m/s2. Calcula su velocidad al cabo de estos dos segundos.
Se conoce la velocidad inicial (4 m/s2), la aceleración (1,5 m/s) y el tiempo (2 s). Aplicando la ecuación de la velocidad final:
Supuesto práctico 7
Un cohete inicialmente parado, se aleja de la Tierra con una aceleración de 5 m/s2. Calcula hasta qué altura habrá ascendido al cabo de 10 segundos.
Se conoce la velocidad inicial (0 m/s), la aceleración (5 m/s) y el tiempo (2 s). Aplicando la ecuación del espacio en relacion a la velocidad y la acelación:

12.1. La representación gráfica del m.r.u.a.
Para el m. r. u. a., se puede representar la variación tanto del espacio, s, como de la velocidad, v, en función del tiempo, t.
La gráfica de la velocidad en un m. r. u. a. es una recta. En cambio, la representación del espacio es una parábola. Para estas representaciones se hallan parejas de puntos (s, t) y (v, t). En las siguientes actividades resueltas se presenta un caso práctico de estas representaciones.
Supuesto práctico 8
Un automóvil circula a 2 m/s y acelera con una aceleración uniforme de 2,5 m/s2 durante 15 segundos. Halla la ¿j representación gráfica del espacio recorrido frente al tiempo empleado.
Calculamos su velocidad en cuatro momentos: en e instante inicial y cada cinco segundos. Denominamos vQI v5, vm y v]5 las velocidades del automóvil cuando har pasado 0 s, 5 s, 10 s y 15 s, respectivamente.
Aplicando la ecuación de la velocidad final: vf = vi+ a · t
Cuando t = 0 s, la vi = 2 m/s,
En nuestra vida cotidiana decimos que aceleramos cuando aumentamos la velocidad y decimos que frenamos cuando disminuimos la velocidad. En realidad, tan cambio de velocidad es un aumento como una disminución. En ambos casos hay una .aceleración Díferenciamos entre:
- Aceleración positiva. Produce aumento de velocidad: la velocidad final es mayor que la inicial. Por ejemplo, cuando un coche pasa de 40 km/h a 80 km/h.
- Aceleración negativa. Produce disminución de velocidad: la velocidad final es menor que la inicial. Por ejemplo, cuando un coche pasa de 70 km/h a 50 km/h
Supuesto práctico 5
Un automóvil pasa de 4 m/s a 8 m/s en un tiempo de 2 segundos. Calcula su aceleración. Calcula también la aceleración para retornara la velocidad inicial en el mismo tiempo de 2 segundos.
El incremento de velocidad es: vf - vi = 8 m/s - 4 m/s = 4 m/s
El tiempo, r, es de 2 s. Así, la aceleración será:

La variación de velocidad es: vf - vi = 4 m/s - 8 m/s = - 4 m/s
El tiempo, t, para este cambio es de 2 s. Así, la aceleración será:

12. MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO
El movimiento rectilíneo y uniformemente acelerado, m. r. u. a., se caracteriza por ser:
- Movimiento rectilíneo. La trayectoria del móvil es una línea recta.
- Movimiento uniformemente acelerado. Su aceleración es constante.
Para saber qué velocidad final, vf , alcanzará a partir de una velocidad inicial, vi , cuando actúe una aceleración, a, durante un tiempo, t, se usa la siguiente igualdad:
vf = vi + a · t
vf = velocidad final
vi = velocidad inicial
a = aceleración
t = tiempo
La igualdad anterior se obtiene de la definición de aceleración, despejando:


v = velocidad inicial
a = aceleración
t = tiempo
Dado que en un MRUA la velocidad varía con el tiempo, para describirlo necesitaremos, además de la posición xi, la velocidad vi en el instante inicial y la aceleración a que actúa sobre el móvil.
Si partimos de la definición de aceleración media:


Para obtener la ecuación de la posición, podemos aprovecharnos del hecho que la velocidad media es constante en el cualquier intervalo, dado que la aceleración es constante. Entonces:



Supuesto práctico 6 |
Se conoce la velocidad inicial (4 m/s2), la aceleración (1,5 m/s) y el tiempo (2 s). Aplicando la ecuación de la velocidad final:
vf = vi + a · t vf = 4 m/s + 1,5 m/s2 · 2 s = 4 m/s + 3 m/s = 7 m/s
Supuesto práctico 7
Un cohete inicialmente parado, se aleja de la Tierra con una aceleración de 5 m/s2. Calcula hasta qué altura habrá ascendido al cabo de 10 segundos.
Se conoce la velocidad inicial (0 m/s), la aceleración (5 m/s) y el tiempo (2 s). Aplicando la ecuación del espacio en relacion a la velocidad y la acelación:

12.1. La representación gráfica del m.r.u.a.
Para el m. r. u. a., se puede representar la variación tanto del espacio, s, como de la velocidad, v, en función del tiempo, t.
La gráfica de la velocidad en un m. r. u. a. es una recta. En cambio, la representación del espacio es una parábola. Para estas representaciones se hallan parejas de puntos (s, t) y (v, t). En las siguientes actividades resueltas se presenta un caso práctico de estas representaciones.
Un automóvil circula a 2 m/s y acelera con una aceleración uniforme de 2,5 m/s2 durante 15 segundos. Halla la ¿j representación gráfica del espacio recorrido frente al tiempo empleado.
Calculamos su velocidad en cuatro momentos: en e instante inicial y cada cinco segundos. Denominamos vQI v5, vm y v]5 las velocidades del automóvil cuando har pasado 0 s, 5 s, 10 s y 15 s, respectivamente.
Aplicando la ecuación de la velocidad final: vf = vi+ a · t
Cuando t = 0 s, la vi = 2 m/s,
Cuando t = 5 s, v5 = vi+ a · t = 2 m/s + 2,5 m/s2 . 5 s= 14,5 m/s
Cuando t = 10 s, v10 = vi+ a · t = 2 m/s + 2,5 m/s2 . 10 s = 27 m/s
Cuando t = 15 s, v15 = vi+ a · t = 2 m/s + 2,5 m/s2 · 15 s = 39,5 m/s
Si se toma unos ejes de coordenadas cartesianos y se representa el tiempo en el eje de las x y la velocidad en el eje de las y, resulta:
La recta no pasa por el origen de coordenadas porque cuando empieza a contar el tiempo (t = 0), el coche ya circulaba a una velocidad de 2 m/s. Si en el momento inicial el coche estuviera parado (v = 0 m/s) la gráfica pasaría por el origen.
Estos valores de velocidad y tiempo podemos resumirlos en la Tabla siguiente:
Si se toma unos ejes de coordenadas cartesianos y se representa el tiempo en el eje de las x y la velocidad en el eje de las y, resulta:
La recta no pasa por el origen de coordenadas porque cuando empieza a contar el tiempo (t = 0), el coche ya circulaba a una velocidad de 2 m/s. Si en el momento inicial el coche estuviera parado (v = 0 m/s) la gráfica pasaría por el origen.
Estos valores de velocidad y tiempo podemos resumirlos en la Tabla siguiente:
| t | v |
| 0 s | 2 m/s |
| 5 s | 14,5 m/s |
| 10 s | 27 m/s |
| 15 s | 39,5 m/s |
Supuesto práctico 9
Para el mismo automóvil de la actividad resuelta anterior que circula a 2 m/s con una aceleración de 2,5 m/s2 durante 15 segundos, representa gráficamente el espacio recorrido frente al tiempo empleado.Calculamos ahora el espacio recorrido también en los mismos tiempos para los que se ha calculado la velocidad.
Denominaremos s0 , s5 , s10 y s15 a los espacios recorridos cuando han pasado 0 s, 5 s, 10 s y 15 s, respectivamente.
Aplicando a cada uno de los tiempos,

Cuando t = 0 s, el espacio:

• Cuando t = 5 s, el espacio

• Cuando t = 10 s, el espacio

• Cuando t = 15 s, el espacio

Si se toman unos ejes de coordenadas cartesianos, se representa el tiempo en el eje de las x, mientras que la velocidad se representa en el eje de las y, resulta:
Al igual que antes, estos valores de espacio y tiempo se pueden reunir en la Tabla 1.5.
| t | s |
| 0 s | 0 m |
| 5 s | 41,25 m |
| 10 s | 145 m |
| 15 s | 311,25 m |
13. LA ACELERACIÓN DE LA GRAVEDADTodo el mundo sabe que los objetos más densos que el aire caen hacia la superficie de la Tierra. En un recinto donde se hubiera extraído el aire incluso objetos como los globos llenos de gas helio (gas más ligero que el aire) o de aire caliente caerían hacia la superficie terrestre.Esta caída de los objetos se debe a la atracción que la Tierra ejerce sobre ellos y es un ejemplo de movimiento uniformemente acelerado. En ausencia de aire, todos los objetos caen con la misma aceleración que se conoce como aceleración de la gravedad, se designa por g y vale 9,8 m/s2 a nivel del mar. Para la caída de los cuerpos bajo la acción de la gravedad sirven las mismas ecuaciones del m.r.u.a. donde la aceleración a tiene el valor de la aceleración de la gravedad (g):
vf = vi + g · t
 vf = velocidqd inicial vi = velocidad inicial t = tiempo g = aceleración de la gravedad Si no fuera por la fricción del aire que afecta más a unos que otros según su forma, todos los cuerpos deberían caer hacia la Tierra con una aceleración de 9,8 m/s2. A medida que nos alejamos de la Tierra la aceleración de la gravedad va disminuyendo y llega a ser cero a distancias muy lejanas. En la Luna, la aceleración con la que caen los cuerpos es menor (1,62 m/s2). En Marte, 3,72 m/s2. En cambio, en Júpiter, el valor de la aceleración de la gravedad se estima en 25,87 m/s2. La aceleración de la gravedad de un planeta depende de la masa de dicho planeta y también de su tamaño. Cuanto mayor masa y menor radío tenga mayor será la gravedad en su superficie. El valor de la gravedad terrestre, g, se toma como referencia para medir aceleraciones. Así, se habla de aceleraciones 2g, 3g, etc. Por ejemplo, en aviones y naves espaciales o en instalaciones donde los pilotos de avión y los astronautas son sometidos a entrenamiento en condiciones extremas. También se usa la comparación con la gravedad terrestre en aparatos de laboratorio conocidos como centrífugas que obtienen «gravedades artificiales» muy superiores a la terrestre y permiten separar los componentes de una mezcla. Supuesto práctico 10 Para calcular la altura de un edificio, se deja caer un objeto desde su azotea y se mide el tiempo, 4 s, que tarda el objeto en llegar al suelo. Calcula la altura del edificio en cuestión y averigua también con qué velocidad llegará al suelo. La velocidad con la que llega al suelo se calcula aplicando la ecuación de la velocidad para el m.r.u.a. En esta ecuación, el valor de la velocidad inicial, vi, es cero porque parte del reposo, o sea, se deja caer, no se lanza hacia abajo. Naturalmente, el valor de la aceleración es el valor de g = 9,8 m/s2 vf = vi+ g · t ; sustituyendo: vf = 0 m/s + 9,8 m/s2· 4 s = 39,2 m/s Para calcular la altura del edificio, se calcula el espacio recorrido por el objeto a partir del tiempo conocido:  Este es el espacio que recorre el objeto hasta impactar en el suelo, o sea la altura del edificio. ANIMACIONES  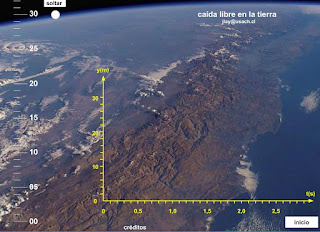       14. MOVIMIENTO CIRCULAR UNIFORME (MCU) La trayectoria es una circunferencia La velocidad es constante Si se considera un punto girando en una circunferencia es fácil concluir que es mucho más sencillo medir el ángulo girado en un intervalo de tiempo que el arco recorrido (espacio). Por esto se define la velocidad angular ω como la rapidez con que se describe el ángulo (ϕ):
Entre la velocidad lineal y la angular
existe la siguiente relación:
El ángulo (ϕ), debe medirse en radianes: Según esta definición:
Otras unidades ( no S.I.) son: vueltas / s ; revoluciones / min = r.p.m De la definición de velocidad angular se deduce la relación entre la velocidad angular ω y el ángulo girado ϕ:
ϕ = ω . t
Si cuando empieza a contarse el tiempo (t = 0) el punto ya ha descrito un ángulo ϕ0, entonces el ángulo girado en un tiempo t será:
El movimiento circular uniforme es un movimiento periódico,
ya que se repite a intervalos regulares de tiempo.
Se denomina periodo ( T ) al tiempo que el punto tarda en dar
una vuelta (el movimiento vuelve a repetirse).
Se denomina frecuencia ( f ) al número de vueltas que el punto
da en un segundo.
Periodo y frecuencia son magnitudes inversamente
proporcionales:
El periodo se mide en segundos (s)
La frecuencia se mide en 1 / s o Hz (hertzios)
Teniendo en cuenta las definiciones de periodo, frecuencia y velocidad angular, se puede poner: La frecuencia es el número de vueltas que da el móvil en 1 s y se representa por f. Como el periodo es el tiempo que tarda en dar una vuelta, la frecuencia es su inverso. 14.1. Aceleración centrípeta En un movimiento; la variación del módulo, la dirección o el sentido del vector velocidad, produce una aceleración. En el MCU, la velocidad lineal, al ser un vector tangente a la trayectoria varia su dirección y sentido a lo largo de la misma. Estos cambios en la velocidad inducen una aceleración perpendicular a la trayectoria,an, a la que denominamos aceleración centrípeta, que es un vector dirigido siempre al centro de la circunferencia:
ANIMACIONES
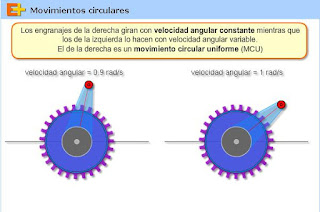
Cuando el movimiento circular descrito por una partícula se rige por una velocidad angular que aumenta de forma constante con el paso del tiempo, se dice uniformemente acelerado (o decelerado, si la velocidad angular decrece con el tiempo). Las ecuaciones que describen este movimiento son las siguientes:
ANIMACIONES
16. MOVIMIENTOS COMPUESTOS Un movimiento cualquiera se puede descomponer en movimientos simples y simultáneos. Este procedimiento simplifica el estudio de los movimientos compuestos. En esta unidad, nos limitaremos al estudio del movimiento compuesto en el plano. Ya Galileo, en el siglo XVI, utilizaba este recurso cuando enunció el principio de independencia de los movimientos. "Cuando un cuerpo sigue un movimiento compuesto por dos movimientos simples y simultáneos, su posición en un tiempo dado es independiente de cómo actúen los movimientos simples, simultánea o sucesivamente". Para estudiar estos movimientos compuestos debemos: Distinguir claramente la naturaleza de cada uno de los movimientos simples componentes. Aplicar a cada movimiento componente sus propias ecuaciones. Obtener las ecuaciones del movimiento compuesto teniendo en cuenta que: La posición de un móvil se obtiene sumando vectorialmente los vectores de posición de los movimientos componentes. La velocidad de un móvil se obtiene sumando vectorialmente los vectores velocidad de los movimientos componentes. El tiempo empleado en el movimiento compuesto, es igual al tiempo empleado en cada uno de los movimientos componentes. 16.1 Navegar por un río. Caracter relativo del movimiento Ya sabemos que el movimiento es diferente según el observador que lo describa. El movimiento es diferente según el sistema de referencia que elijamos. Cuando decimos que un vehículo marcha a 40 km/h, queremos decir que se mueve con una velocidad de 40 km/h respecto a un observador quieto situado fuera del vehículo. Respecto a un pasajero, lo que se mueve es la carretera. En resumen decimos que el movimiento es relativo. Aclaremos qué significa que el movimiento es relativo con un ejemplo: Supongamos que dos personas navegan en una barca, una sentada delante y otra detrás. Para medir la velocidad de la barca, al pasar por un tramo recto del río, hacemos dos marcas separadas 50 m y observamos que la barca tarda 5 s en recorrer esa distancia. Según nuestros cálculos, las personas de la barca se mueven con una velocidad de 50 m / 5 s =10 m/s, relativa a nosotros (o a la Tierra). La persona que va sentada detrás en la barca, observa que durante ese tiempo, la persona de delante no se ha movido con respecto a él, es decir mide una velocidad de 0 m/ 5 s = 0 m/s relativa a él (o la barca). Entonces, ¿cuál es la velocidad correcta del pasajero? La velocidad correcta o verdadera de un cuerpo no existe. Ambas velocidades son correctas, cada una en su sistema de referencia. 16.2. Cruzar un río. Un movimiento compuesto Imaginemos una barca con la que el remero pretende cruzar el río perpendicularmente a las orillas. La barca es desviada por la corriente del río, de manera que su trayectoria es una recta que forma un ángulo α con la orilla. El movimiento real de la barca está compuesto por: Un MRU perpendicular a las orillas del río, debido al esfuerzo de los remeros. Un MRU paralelo a las orillas, debido a la corriente del río. 16.3 Tiro parabólico. Otro movimiento compuesto Consideremos un cañón que dispara un obús desde el suelo con cierto ángulo α menor de 90º con la horizontal. El obús experimenta un movimiento de subida y bajada a lo largo del eje Y y un movimiento de avance a lo largo del eje X. A lo largo del eje X es un MRU horizontal de velocidad Vox constante. A lo largo del eje Y es Un MRUA vertical con velocidad inicial Voy hacia arriba. La composición de un movimiento uniforme y otro uniformemente acelerado resulta un movimiento cuya trayectoria es una parábola. Este movimiento está estudiado desde la antigüedad. Se recoge en los libros más antiguos de balística para aumentar la precisión en el tiro de un proyectil. Denominamos proyectil a todo cuerpo que una vez lanzado se mueve solo bajo la aceleración de la gravedad.
16.4. Tiro parabólico con altura inicial
Consideremos ahora que el cañón dispara un obús desde una altura h y un ángulo α menor de 90º con la horizontal.
Al igual que en el caso anterior, el obús, experimenta un movimiento de subida y bajada a lo largo del eje Y (MRUA) y un movimiento de avance a lo largo del eje X (MRU).
Recuerda la escena "Tiro parabólico. Otro movimiento compuesto."
Para alcanzar el tanque, era necesario ajustar la velocidad y el ángulo de lanzamiento.
Ahora el tanque esta a cierta altura sobre el suelo. ¿Serán necesarias las mismas condiciones de velocidad y ángulo e lanzamiento o la altura tiene algo que ver?
Compruébalo con la escena:
ANIMACIONES
17. TIRO PARABÓLICO
Cuando lanzamos un cuerpo con una velocidad que forma un ángulo con la horizontal, éste describe una trayectoria parabólica. En su obra Dialogo sobre los Sistemas del Mundo (1633), Galileo Galilei expone que el movimiento de un proyectil puede considerarse el resultado de componer dos movimientos simultáneos e independientes entre sí: uno, horizontal y uniforme; otro, vertical y uniformemente acelerado.
En nuestra simulación hemos seleccionado el punto de salida como origen de coordenadas. Si la velocidad de salida es v0 y el ángulo es α, tendremos que las componentes de la velocidad inicial son:
v0x = v0· cos α
v0y = v0· sen α
Y las propiedades cinemáticas del cuerpo en cualquier instante (t) de su movimiento son:
Observa que la aceleración no depende del tiempo (es constante), pero la velocidad y la posición del móvil sí que dependen del tiempo. En el tiro parabólico son de interés la altura máxima y el alcance (o desplazamiento horizontal) conseguido.
La altura máxima se alcanza cuando la componente vertical vy de la velocidad se hace cero. Como
vy = v0y - gt,
se alcanzará la altura máxima cuando
t = v0y/g.
Utilizando estos datos llegarás fácilmente a la conclusión de que el valor de la altura máxima es:
ymax= v0y2/2g = (v02/2g) sen2α
El móvil estará avanzando horizontalmente a la velocidad constante v0x durante el tiempo de vuelo, que será 2t (siendo t el tiempo en alcanzar la altura máxima) ya que el móvil tarda lo mismo en subir que en bajar, por lo tanto el alcance es:
xmax = v0x2t
es decir
alcance = xmax = (v02/g) sen 2α
18. LANZAMIENTO EN LA VERTICAL
Movimiento uniformemente variado, donde la aceleración es la de la gravedad y la dirección del movimiento puede ser ascendente o descendente, sin influencia de la fricción con el aire.
a = g
v0 ≠ 0
Este movimiento siempre tiene velocidad inicial distinta de cero, sea lanzado hacia arriba o hacia abajo.
Las ecuaciones para éste movimiento son: 1) yf = y0 + v0.t + ½.g.t² Ecuación de posición 2) vf = v0 + g.t Ecuación de velocidad 3) vf² = v0² + 2.g.Δy Altura Máxima: El único instante donde la velocidad es nula es cuando alcanza la altura máxima, si el objeto o móvil fue lanzado hacia arriba. Es el punto donde el objeto se detiene y comienza el descenso. Ecuaciones para el caso de calcular la altura máxima: 1) y Máxima = y0 + v0.t + ½.g.t² Ecuación de posición 2) 0 = v0 + g.t Ecuación de velocidad 3) 0 = v0² + 2.g.Δy Velocidad Inicial: Una particularidad del tiro vertical es que un objeto lanzado hacia arriba con una determinada velocidad inicial, al regreso y pasando por el mismo punto de partida, posee el mismo valor de velocidad pero con sentido contrario al del lanzamiento. El valor de la aceleración de la gravedad depende del paralelo (latitud) en que se determine dicho valor. En el ecuador (latitud = 0) la aceleración es igual a “9,78049 m/s²”, la aceleración promedio es de 9,81 m/s², es usual usar un valor de 10 m/s² para agilizar la resolución de ejercicios. Ejes convenientes para graficar el movimiento:
Orientación de los vectores y selección de los signos de las variables según la dirección del movimiento:
Estos signos se deben aplicar cuando se reemplazan las variables por sus valores. Nota: si la velocidad inicial es nula (v0 = 0) se trata de “Caída Libre”. ANIMACIONES
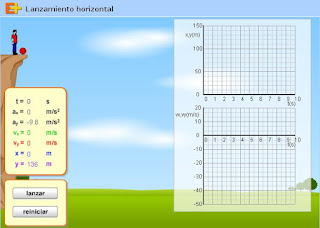
19. TIRO HORIZONTAL
El movimiento que realiza la moto en la siguiente simulación es una rama de parábola y se llama tiro horizontal.
Si la velocidad de salida es v0, tendremos que las componentes de la velocidad inicial son:
v0x = v0
v0y = 0
Como ocurría en el caso del tiro parabólico, este movimiento puede considerarse el resultado de componer dos movimientos simultáneos e independientes entre sí: uno, horizontal y uniforme; otro, vertical y uniformemente acelerado. Las propiedades cinemáticas del cuerpo en cualquier instante (t) de su movimiento son:
Combinando las ecuaciones podemos llegar a la conclusión de que el tiempo de vuelo es:
t = ( 2h/g)½
y por lo tanto el desplazamiento horizontal alcanzado es:
xmax = v0 ( 2h/g)½
Observa que el tiempo de vuelo no depende de la velocidad, sino de la altura y del valor de la gravedad.
20. RESUMEN
Todos los cálculos relacionados con las magnitudes que describen los movimientos rectilíneos podemos hacerlos con estas dos ecuaciones:
Si el móvil parte del orígen de coordenadas
Significa que la posición inicial eo del cuerpo es cero. En este caso la ecuación del desplazamiento podemos escribirla así:
Si el móvil parte del reposo
Esto quiere decir que la velocidad inicial es cero. Al sustituir este valor en las ecuaciones anteriores, queda:
Si el movimiento es uniforme
Es el movimiento de velocidad constante, es decir el movimiento con aceleración cero.
Al dar valor 0 a la aceleración, las ecuaciones del principio quedan así:
Ya habrás notado que no se trata de ecuaciones diferentes sino de las mismas ecuaciones adaptadas a dos casos concretos, por tanto no es necesario que aprendas de memoria todas las ecuaciones: con las dos primeras y un análisis de la situación tienes suficiente.
Cómo resolver los ejercicios
Para resolver un ejercicio no basta con aplicar las ecuaciones. Es necesario seguir un método o estrategia que podemos resumir así:
21. PRÁCTICAS
Gráficas e-t
Vamos a ver cómo podemos utilizar las gráficas posición-tiempo para describir el movimiento. Podemos deducir las características de un movimiento analizando la forma y la pendiente de las gráficas posición-tiempo (e-t). La pendiente de una gráfica e-t representa la velocidad del móvil.Si el movimiento es uniforme, la gráfica e-t es una recta ya que en tiempos iguales se producen desplazamientos iguales. Comprueba en el siguiente simulador que la pendiente de la gráfica representa la velocidad.
Gráfica v-t
En una gráfica v-t, la pendiente es la aceleración. En el siguiente simulador podemos hacer que las motos se muevan a velocidad constante. Observa que al representar los datos en la gráfica v-t se obtiene una recta horizontal, cuya pendiente es cero en todos los puntos, ya que en los movimientos uniformes no hay aceleración (la aceleración es cero).La forma de la gráfica velocidad-tiempo para estos dos tipos de movimientos revela una importante información:
        22. CUESTIONES 
23. VÍDEOS Vídeo 1 Sistemas de referencia Movimiento Vector de posición Movimiento Tipos de movimiento Ejercicios Ejercicio resuelto Como se mueven las cosas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||













































































































No hay comentarios:
Publicar un comentario