ÍNDICE
|
10. Potencia
11. Rendimiento energético
12. ¿Qué es el calor?
1. Formas de transmisión del calor
1. Conducción
2. Covección
3 Radiación
13. Los efectos del calor
1. La variación de la temperatura
2. La dilatación y contracción
3. Cambios de estado
14. ¿Qué es la temperatura?
1. La medida de la temperatura
15. Máquinas
1. Palancas
2. Poleas
3. Otras máquinas
16. Resumen
17. Prácticas
18. Cuestiones
19. Vídeos
|
1. ESQUEMAS

2. PRESENTACIONES
3. CONTENIDOS ANIMADOS
Esta unidad introduce dos magnitudes relacionadas, el trabajo y la energía.
Definiremos primero el concepto de trabajo porque puede hacerse a partir de los conceptos de fuerza y desplazamiento que se han estudiado en las unidades anteriores. Luego se introducirá el concepto de energía a partir del de trabajo.
4.1. Si no hay cambios, no hay trabajo
Las fuerzas son interacciones entre los cuerpos. Pero no basta que un cuerpo ejerza una fuerza sobre otro para que haya consecuencias. Para medir las consecuencias de la acción de las fuerzas en un sistema se usa el trabajo.
El trabajo es una medida de la acción que las fuerzas hacen sobre un sistema.
Para que se produzca trabajo es necesario que las fuerzas «hagan algo». Cuando las fuerzas no consiguen cambiar alguna cosa se dice que «no trabajan».
No hay trabajo si después de los cambios el sistema recupera la forma o posición iniciales.
Empujar una pared sin conseguir moverla o derribarla no es trabajo, levantar unas pesas del suelo y dejarlas en el mismo sitio no es trabajo, y estirar un muelle elástico y dejarlo volver a la posición inicial tampoco es trabajo (Figura 2).
Sí que es trabajo: empujar una vagoneta cambiándola de sitio, subir un saco de arena a un piso y dejarlo allí o doblar una barra de hierro (Figura 3).
| Figura 2. Tres situaciones en las que, a pesar del esfuerzo no hay trabajo. | ||
| Figura 3. Tres situaciones en las que las fuerzas realizan trabajo. | ||
El concepto físico de trabajo de una fuerza no es el mismo que el de «hacer fuerza». Nadie duda de que quien empuja con ahínco una pesada vagoneta está haciendo fuerza, pero si no consigue moverla el trabajo realizado es nulo. Hay tantos tipos de trabajo como tipos de fuerzas: Habrá trabajo gravitatorio si interviene la fuerza de la gravedad, trabajo eléctrico si interviene la fuerza eléctrica, trabajo magnético si se trata de fuerzas magnéticas, etc. La mecánica es la parte de la física que se ocupa del movimiento de los cuerpos y de sus causas. Trabajo mecánico es el que se realiza al cambiar la posición o el movimiento de los cuerpos. 4.2. ¿Cómo se calcula el trabajo mecánico? ¿Se puede cuantificar el trabajo? ¿Podemos medir el trabajo? La respuesta es sí, pero no hay un aparato medidor de trabajo, es una magnitud que se mide de forma indirecta. El trabajo efectuado por una fuerza se calcula a partir del valor de la fuerza y de los efectos producidos. Si empujamos una vagoneta con una fuerza, F,durante una distancia, s, se produce trabajo porque la acción de la fuerza ha movido el carro (Figura 8): Supongamos, en general, un cuerpo que se mueve bajo la acción de una fuerza constante F, siguiendo una trayectoria rectilínea y recorriendo una distancia s desde el punto de coordenada s1 al punto de coordenada s2 (Figura 3.6): |
Figura 39. Factores de los que depende el trabajo de desplazamiento. |
Siempre que la fuerza se ejerza en la misma dirección que el movimiento, se define como trabajo, W, al producto de la fuerza, F, por el desplazamiento, s:
W = F • s
En general:
La unidad de trabajo en el Sistema Internacional es el joule (J) (en castellano julio) en honor del científico James Prescott Joule, quien estudió la conversión de calor en trabajo y viceversa.
Según la definición de trabajo, 1 joule es igual al trabajo que realiza una fuerza de 1 Newton a lo largo de 1 metro de recorrido.
El trabajo puede tener signo positivo o negativo:
Si la fuerza actúa en el mismo sentido que el movimiento, el trabajo es positivo. Por ejemplo, el trabajo del motor de un coche que impulsa el vehículo en el sentido de la marcha.
Si la fuerza actúa en sentido contrario al movimiento, realiza un trabajo negativo, como ocurre con el trabajo que realizan los frenos de un vehículo cuando ejercen una fuerza contra del movimiento.
Figura 10. Sobre una vagoneta (a) que se mueve a una velocidad, v, una fuerza, F puede realizar trabajo positivo (b) o negativo (c). |
| Supuesto práctico 1 Una persona, con la ayuda de una polea, levanta una masa de 50 kg hasta una altura de 10 m (Figura 11). Calcula el trabajo realizado. La fuerza que la persona debe hacer para levantar el cuerpo de masa m es, como mínimo, igual al peso de dicha masa:
P = m • g = 50 kg • 9,8 m/s2 = 490 N
Y esta fuerza actúa a lo largo de 10 m. Por tanto:
W = F • h = 490 N • 10 m = 4900 J
| Figura 11. |
| Supuesto práctico 2 Un carro de forraje se mueve a velocidad constante tirado horizontalmente por un caballo con una fuerza de 1 000 N. Calcula el trabajo que ha realizado el caballo cuando el carro ha recorrido 20 m en línea recta (Figura 11). Según la definición de trabajo mecánico, este será:
W = F • s
Y sustituyendo:
W = 1 000 N • 20 m = 20000 J
Su velocidad constante indica que este trabajo se utiliza para contrarrestar el trabajo de las fuerzas de fricción, que es un trabajo negativo pues se opone al movimiento. | |
Figura 11. | |


5. ¿QUÉ ES LA ENERGÍA?
La energía es otro concepto físico común en nuestras vidas. Decimos que la energía del petróleo mueve los automóviles, y que la energía de los alimentos nos permite realizar actividades físicas. De alguien muy activo se dice que «tiene mucha energía». Es decir, en el lenguaje cotidiano, «tener mucha energía» significa que podemos «trabajar mucho». El concepto físico de energía es el siguiente:
La energía es la capacidad de los cuerpos o sistemas para realizar trabajo.
La energía se mide en las mismas unidades que el trabajo, joules, en el S.I. Otras unidades son las calorías (cal) y los kilovatio/hora (kWh). La energía que poseen los cuerpos tiene dos propiedades destacadas:
- La energía puede transferirse de un sistema a otro. Por ejemplo, si chocan dos bolas, parte o toda la energía de la una se transmite a la otra.
- La energía puede transformarse de un tipo en otro de los muchos que existen. Así, la energía solar en eléctrica y esta en energía calorífica.
- Cinética, si permite cambiar el movimiento de los cuerpos.
- Potencial, si cambia la altura de los cuerpos respecto al nivel del suelo.
| 1 cal = 4,18 J |
| 1 Kwh = 3.600.000 J = 3,6 106 J |
Los tipos de energía son:
ANIMACIONES
Si una bola de billar se lanza contra otra bola quieta, la pondrá en movimiento, si se lanza contra un cristal probablemente lo romperá, y si se lanza contra un bloque de plastilina, lo deformará.
La bola es capaz de realizar trabajo. Luego tiene energía. Esta energía que depende de la masa de los cuerpos y de su velocidad es la energía cinética (Figura 12).
La energía cinética es la energía que poseen los cuerpos debido a su movimiento. Depende de la masa del cuerpo y de su velocidad.
La energía cinética, Ec, se define como:

v = velocidad del cuerpo
Si un trabajo cambia la energía cinética de un cuerpo, dicho trabajo es igual a la energía cinética final, Ecf , menos la energía cinética inicial, Eci .

| Figura 12. La energía cinética depende de la velocidad y de la masa. Si circulan a la misma velocidad, la energía cinética de la motocicleta es menor que la del automóvil y la de este menor que la del camión. | ||
AN9MACIONES
5.2. La energía potencialSi una roca situada en la ladera de una montaña se desprende, en su caída puede golpear otras rocas y ponerlas en movimiento, puede abollar un refugio de montaña o un vehículo que esté en la falda de la montaña, puede, en definitiva, realizar trabajo. Si puede realizar trabajo es porque la roca en una situación elevada tenía energía. Este tipo de energía que depende de la posición respecto al suelo de los cuerpos se conoce como energía potencial gravitatoria o simplemente energía potencial.La energía potencial gravitatoria de un cuerpo es la energía debida a su posición. Depende de la masa del cuerpo y de su altura sobre el suelo. La energía potencial, Ep, se define como el producto de la masa de un cuerpo, m, por el valor de la gravedad, g, por la altura a la que el cuerpo esté situado sobre el suelo, h (Figura 13):
Ep = m • g • h
Supongamos que un trabajo, W, sirve para que un cuerpo cambie su altura respecto al suelo, este trabajo realizado será igual a la energía potencial final (Epf = m • g • hf) menos la energía potencial inicial (Epi = m • g • hi) (Figura 14):
W = Epf - Epi = m • g • hf - m • g • hi =
m • g • ( hf - hi)
ES decir:
W = m • g • ( hf - hi)
Se mide en las mismas unidades que el trabajo y que la energía cinética: joules (J) en el Sistema Internacional. |
Figura 13. Para que un cuerpo pase de una altura hi. a una hf, se debe realizar una fuerza F igual a su peso, m • g, a lo largo de la altura, hf - hi..
El trabajo realizado será: F • ( hf - hi)
Es decir: W = m • g • ( hf - hi) = Epf - Epi .
|
Figura 14. En el primer dibujo, el saco de masa m no tiene energía potencial ni cinética. En el segundo dibujo, el saco ha adquirido una energía potencial gracias al trabajo del operario. En el tercer dibujo, el saco se ha soltado y va perdiendo energía potencial (al perder altura) pero va ganando energía cinética al ganar velocidad.
|
Supuesto práctico 3
Calcula la energía cinética que posee un automóvil de 800 kg de masa que circula a 120 km/h (Figura 15). Se deben convertir las unidades de velocidad a unidades del S.l. (m/s). La energía cinética es: Supuesto práctico 4 Calcula la energía potencial gravitatoria que posee un cubo de agua de 8 kg de masa situado en un andamio a 4 m de altura sobre el suelo.
Ep = m • g • h = 8kg • 9,8 m/s2 • 4 m = 313,6 J
Supuesto práctico 5 Calcula el trabajo necesario para subir un saco de arena de 50 kg de masa desde la calle hasta la azotea de un edificio de 100 m de altura. En el cálculo de la energía potencial se tomará como cero la altura a nivel de la calle: La energía potencial inicial es:
Ep = m • g • h = 800 kg • 9,8 m/s2 • 0 m = 0 J
La energía potencial final es:
Epf = m • g • hf = 800 kg • 9,8 m/s2 • 100 m = 784000 J
W = Epf - Epi = 784 000 J - 0 J = 784 000 J
Supuesto práctico 6 Un automóvil de 800 kg pasa de 20 km/h a circular a 80 km/h. a) Calcula su energía cinética inicial y final. b) Calcula el trabajo realizado por el motor. Se deben convertir las unidades de velocidad a unidades del S.l. (m/s):
La energía cinética inicial es:
La energía cinética final es: El trabajo del motor:
W = Epf - Epi = 197530,86 J - 12 345,68 J = 185 185,18 J
|
5.3. Energía elástica
La energía potencial es, junto con la energía cinética, el otro tipo de energía mecánica que pueden tener los cuerpos. A diferencia de la energía cinética, la energía potencial está asociada a la posición que tienen los cuerpos, y no a su movimiento.
Definimos laenergía potencial como aquella que poseen los cuerpos por el hecho de encontrarse en una determinada posición en un campo de fuerzas.
La energía potencial es, junto con la energía cinética, el otro tipo de energía mecánica que pueden tener los cuerpos. A diferencia de la energía cinética, la energía potencial está asociada a la posición que tienen los cuerpos, y no a su movimiento.
¿Has jugado alguna vez al pinball? Para poner la bola en juego es necesario que comprimas el lanzador. Una vez comprimido, puedes mantenerlo en esa posición todo el tiempo que desees. La bola permanecerá en reposo. Sin embargo, una vez liberado, el lanzador (un muelle), transforma el estado de reposo de la bola, y esta se pone en movimiento. El resto depende de tu habilidad y tu suerte para evitar que la pelota caiga del tablero de juego. En cualquier caso, lo importante es señalar que el muelle deformado cuenta con una energía (capacidad para producir un trabajo, una transformación) por el hecho de encontrarse desplazado (comprimido o estirado) respecto a su posición de equilibrio.
Definimos la energía potencial elástica como aquella que adquieren los cuerpo sometidos a la acción de fuerzas elásticas o recuperadoras. En el caso de un cuerpo unido a un muelle su valor viene dado por:
Ep: Es la energía potencial del cuerpo. Su unidad de medida en el Sistema Internacional es el Julio (J)
k: Constante elástica del muelle. Depende el propio muelle en sí, cuanto mayor es su valor, más trabajo cuesta estirar el muelle. Su unidad de medida en el Sistema Internacional es Newton por metro (N/m)
x: Distancia hasta la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m)
5.4. Energía mecánica
Son innumerables los casos en los que el trabajo modifica, simultáneamente, la energía cinética y la energía potencial de un cuerpo. Es decir, modifica la energía mecánica en su conjunto.
Si sobre un cuerpo actúa una fuerza que provoca cambios en su velocidad y en su posición, el trabajo de esa fuerza será igual a la variación de energía mecánica que sufre el cuerpo.
W = ΔEM =(Ep2+Ec2)-(Ec1+ Ep1)
6. LA CONSERVACIÓN DE LA ENERGÍA MECÁNICA
Lanzamos una pelota al aire vertlcalmente y hacia arriba y seguimos la subida y bajada de la pelota y sus variaciones de energía cinética y potencial (Figura 16):
Cuando parte del nivel del suelo, toda su energía es energía cinética que se le ha comunicado al lanzarla.
A medida gue va subiendo, pierde velocidad, con lo que disminuye su energía cinética; pero gana altura, con lo que aumenta su energía potencial.
Cuando llega al punto más alto, su energía potencial es máxima. En cambio, su energía cinética es cero porque su velocidad también es cero.
En el camino de bajada va perdiendo energía potencial pues pierde altura pero va ganando energía cinética porque adquiere velocidad.
Al llegar al suelo, su energía potencial es cero pues su altura es cero. En cambio, su energía cinética (y su velocidad) vuelven a ser las que tenía al partir.
Si sobre un cuerpo no actúa ningún motor o causa que aporte o reste trabajo, al perder energía cinética, la gana como energía potencial y viceversa (Figura 17).
La suma de sus energías Ec y Ep vale siempre lo mismo. Es el principio de conservación de la energía mecánica:
Principio de conservación de la energía mecánica: Si no hay aporte o pérdida de trabajo, la energía mecánica (cinética más potencial) de un cuerpo se mantiene constante.
Emecánica = Ecinética + Epotencial = constante
Dicho de otro modo: la suma de energías cinética y potencial que un cuerpo poseía al principio es igual a la suma de las mismas energías que posee al final:
Eci + Epi = Ecf + Epf
Observa cuál es el valor de la energía cinética y de la potencial en diferentes puntos de la trayectoria de un carro en una montaña rusa:






ANIMACIONES


Supuesto práctico 7
Un automovilista circula a 80 km/h cuando enfila una pendiente y, al mismo tiempo, pone en punto muerto el motor del coche. La masa del coche y su ocupante es de 900 kg. Calcula hasta qué altura podrá subir el automóvil por la pendiente (Figura 3.16).
La velocidad inicial debe pasarse a unidades del S.l

Para la energía potencial se toma como cero la altura del nivel de la carretera antes de iniciar la pendiente:
La energía cinética Inicial es:

La energía potencial final queda en función de la altura a la que llega, que es la Incógnita del problema:
La energía cinética final es cero porque el coche se para en el punto más alto al que llega:

Según el principio de conservación de la energía mecánica, la suma de las energías cinética y potencial iniciales ha de ser igual a la suma de las finales.
Un automovilista circula a 80 km/h cuando enfila una pendiente y, al mismo tiempo, pone en punto muerto el motor del coche. La masa del coche y su ocupante es de 900 kg. Calcula hasta qué altura podrá subir el automóvil por la pendiente (Figura 3.16).
La velocidad inicial debe pasarse a unidades del S.l
Para la energía potencial se toma como cero la altura del nivel de la carretera antes de iniciar la pendiente:
Epi = m • g • hi= 900 kg • 9,8 m/s2 • 0 m = 0 J
La energía potencial final queda en función de la altura a la que llega, que es la Incógnita del problema:
Epf = m • g • hf = 900 kg • 9,8 m/s2 • hf = 8820 hf J
La energía cinética final es cero porque el coche se para en el punto más alto al que llega:
Según el principio de conservación de la energía mecánica, la suma de las energías cinética y potencial iniciales ha de ser igual a la suma de las finales.
Eci + Epi = Ecf + Epf
222 222,2 J + 0 J = 0 J + 8820 hf
De donde se halla: h.
Esta es la altura máxima a la que podría llegar. En realidad será un poco menor debido a las fuerzas de fricción, que en este problema se han omitido.
Supuesto práctico 8
| Una bola de acero de 100 g de masa se deja caer desde 10 m de altura. Calcula con qué velocidad llegará al suelo suponiendo que la resistencia del aire sea nula. Calculemos la energía cinética y potencial de la bola tanto al dejarla caer como al llegar al suelo. Hay que prever el paso de la masa a unidades del Sistema Internacional: | Figura 19. |
La energía potencial inicial es:
Epi = m • g • hi= 0,1 kg • 9,8 m/s2 • 10 m = 9,8 J
La energía cinética final no puede calcularse porque no sabemos la velocidad con que llega al suelo, gue es precisamente la incógnita del problema. El valor de Ecf se deja en función de la velocidad final, vf :
La energía potencial final es cero porque la altura sobre el suelo es cero:
Epf = m • g • hf= 0,1 kg • 9,8 m/s2 • 0 m = 0 J
Por el principio de conservación de la energía mecánica, las energías cinética y potencial deben sumar lo mismo al principio que al final.
Eci + Epi = Ecf + Epf
0 J + 9,8 J = 0,05 vf2 J + 0 J
9,8 J = 0,05 vf2 J
De donde se halla:
Esta es la velocidad con la que la bola llega al suelo.
6.1. Péndulo
Llamamos péndulo a todo cuerpo que puede oscilar con respecto de un eje fijo.
Péndulo ideal, simple o matemático: Se denomina así a todo cuerpo de masa m (de pequeñas dimensiones) suspendido por medio de un hilo inextensible y sin peso. Estas dos últimas condiciones no son reales sino ideales; pero todo el estudio que realizaremos referente al péndulo, se facilita admitiendo ese supuesto .
Péndulo físico: Si en el extremo de un hilo suspendido sujetamos un cuerpo cualquiera , habremos construido un péndulo físico. Por esto, todos los péndulos que se nos presentan (columpios, péndulo de reloj, una lámpara suspendida, la plomada) son péndulos físicos.
Llamamos péndulo a todo cuerpo que puede oscilar con respecto de un eje fijo.
Péndulo ideal, simple o matemático: Se denomina así a todo cuerpo de masa m (de pequeñas dimensiones) suspendido por medio de un hilo inextensible y sin peso. Estas dos últimas condiciones no son reales sino ideales; pero todo el estudio que realizaremos referente al péndulo, se facilita admitiendo ese supuesto .
Péndulo físico: Si en el extremo de un hilo suspendido sujetamos un cuerpo cualquiera , habremos construido un péndulo físico. Por esto, todos los péndulos que se nos presentan (columpios, péndulo de reloj, una lámpara suspendida, la plomada) son péndulos físicos.
Los parámetros que pueden medirse son: Oscilación – Amplitud – Período y Frecuencia:
A continuación estudiaremos una serie de procesos que ocurren durante la oscilación de los péndulos y que permiten enunciar las leyes del péndulo.
Daremos previamente los siguientes conceptos:
 Longitud del péndulo (L) es la distancia entre el punto de suspensión y el centro de gravedad del péndulo.
Longitud del péndulo (L) es la distancia entre el punto de suspensión y el centro de gravedad del péndulo.
Oscilación simple es la trayectoria descrita entre dos posiciones extremas (arco AB).
A continuación estudiaremos una serie de procesos que ocurren durante la oscilación de los péndulos y que permiten enunciar las leyes del péndulo.
Daremos previamente los siguientes conceptos:
Oscilación simple es la trayectoria descrita entre dos posiciones extremas (arco AB).
Oscilación completa o doble oscilación es la trayectoria realizada desde una posición extrema hasta volver a ella, pasando por la otra extrema (arco ABA). Angulo de amplitud o amplitud (alfa) es el ángulo formado por la posición de reposo (equilibrio) y una de las posiciones extremas.
Período o tiempo de oscilación doble (T) es el tiempo que emplea el péndulo en efectuar una oscilación doble.
Tiempo de oscilación simple (t) es el tiempo que emplea el péndulo en efectuar una oscilación simple.
Elongación (e). Distancia entre la posición de reposo OR y cualquier otra posición.
Máxima elongación: distancia entre la posición de reposo y la posición extrema o de máxima amplitud.
Frecuencia (f). Es el número de oscilaciones en cada unidad de tiempo.
f=numero de oscilaciones/tiempo
Relación entre frecuencia y periodo
Supongamos un péndulo que en 1 seg. cumple 40 oscilaciones.
En consecuencia: 40 oscilaciones se cumplen en 1 seg., por lo que 1 osc. se cumple en T=1/40 seg (periodo) .
Obsérvese que: el período es la inversa de la frecuencia.
En símbolos: T= 1 / f y f= 1 / T
Leyes del péndulo:
1. Ley de las masasLas tres mas de la figura son distintas entre si, pero el periodo (T) de
oscilación es el mismo. (T1=T2=T3)
Los tiempos de oscilación de varios péndulos de igual longitud son independientes de sus masas y de su naturaleza, o también El tiempo de oscilación de un péndulo es independiente de su masa y de su naturaleza.
Dispongamos dos de los péndulos empleados en el experimento anterior. Separémolos de sus posiciones de equilibrio, de tal modo que los ángulos de amplitud sean distintos (pero no mayores de 6 o 7 grados).
Dejémolos libres: comienzan a oscilar, y notaremos que, también en este caso, los péndulos “van y vienen” al mismo tiempo. De esto surge la llamada Ley del isocronismo (iguales tiempos):
Para pequeños ángulos de amplitud, los tiempos de oscilación de dos péndulos de igual longitud son independientes de las amplitudes, o también: El tiempo de oscilación de un péndulo es independiente de la amplitud (o sea, las oscilaciones de pequeña amplitud son isócronas).
Dejémolos libres: comienzan a oscilar, y notaremos que, también en este caso, los péndulos “van y vienen” al mismo tiempo. De esto surge la llamada Ley del isocronismo (iguales tiempos):
Para pequeños ángulos de amplitud, los tiempos de oscilación de dos péndulos de igual longitud son independientes de las amplitudes, o también: El tiempo de oscilación de un péndulo es independiente de la amplitud (o sea, las oscilaciones de pequeña amplitud son isócronas).
Ley de las longitudes:
Suspendamos ahora tres péndulos cuyas longitudes sean:
Péndulo A = (10cm) 1 dm.
Péndulo B = (40 cm) 4 dm.
Péndulo C = (90 cm) = 9 dm.
1) El de 1 dm. y el de 4dm.
2) El de 1 dm. y el de 9dm.
Observaremos entonces que:
a) El de menor longitud va más ligero que el otro, o sea: “a menor longitud menor tiempo de oscilación y a mayor longitud mayor tiempo de oscilación”.
b) Mientras el de 4 dm. cumple una oscilación, el de 1 dm. cumple dos oscilaciones.
c) Mientras el de 9 dm. cumple una oscilación, el de 1 dm. cumple tres oscilaciones.
Esta circunstancia ha permitido establecer la siguiente ley de las longitudes:
Los tiempos de oscilación (T) de dos péndulos de distinta longitud (en el mismo lugar de la Tierra), son directamente proporcionales a las raíces cuadradas de sus longitudes.
En símbolos
T1 y T2: tiempos de oscilación;
l1 y l2 : longitudes.
Para nuestro caso es:
T1= 1 oscilación y l1= 1dm
T2 = 2 oscilaciones y l2 =4 dm
luego:
 T1=1 oscilación y l1=1
T1=1 oscilación y l1=1
T3=3 oscilaciones y l3=9
luego:
Al estudiar el fenómeno de la oscilación dejamos aclarado que la acción gravitatoria tiende a hacer parar el péndulo, pues esa es la posición más cercana a la Tierra. Significa esto, en principio, que la aceleración de la gravedad ejerce una acción primordial que evidentemente debe modificar el tiempo de oscilación del péndulo.
Si tenemos presente que la aceleración de la gravedad varía con la latitud del lugar, resultará que los tiempos de oscilación han de sufrir variaciones según el lugar de la Tierra.
En efecto, al experimentar con un mismo péndulo en distintos lugares de la Tierra (gravedad distinta) se pudo comprobar que la acción de la aceleración de la gravedad modifica el tiempo de oscilación del péndulo.
Por ejemplo: si en Buenos Aires el tiempo de oscilación es T1, y la gravedad g1, en Río de Janeiro el tiempo de oscilación es T2 y la gravedad g2, se verifica la siguiente proporcionalidad:

Los tiempos de oscilación de un mismo péndulo en distintos lugares de la Tierra son inversamente proporcionales a las raíces cuadradas de las aceleraciones de la gravedad.
Fórmula del tiempo de oscilación del péndulo:
Para poder obtener el tiempo de oscilación de un péndulo se aplica la siguiente expresión:

Si fuera el correspondiente para una oscilación simple, aplicamos:

Esta fórmula condensa en sí las cuatro leyes del péndulo. En efecto, observamos
1) En esa expresión no figura la masa m del péndulo, por lo que “el tiempo de oscilación es independiente de la masa”.
2) Como tampoco figura el ángulo de amplitud, “el tiempo de oscilación es independiente de la amplitud”.
3) La 3ra. y 4ta. leyes están incluidas en el factor:
 El péndulo y sus aplicaciones:
El péndulo y sus aplicaciones:
Las aplicaciones del péndulo son variadas. Las más importantes son:
a) Determinación de la aceleración de la gravedad.
Sabemos que:



b) Determinación del movimiento de rotación de la Tierra
Si tenemos presente que la aceleración de la gravedad varía con la latitud del lugar, resultará que los tiempos de oscilación han de sufrir variaciones según el lugar de la Tierra.
En efecto, al experimentar con un mismo péndulo en distintos lugares de la Tierra (gravedad distinta) se pudo comprobar que la acción de la aceleración de la gravedad modifica el tiempo de oscilación del péndulo.
Por ejemplo: si en Buenos Aires el tiempo de oscilación es T1, y la gravedad g1, en Río de Janeiro el tiempo de oscilación es T2 y la gravedad g2, se verifica la siguiente proporcionalidad:
Repitiendo los experimentos para lugares de distinta latitud (por tanto, distinta gravedad) se puede verificar proporcionalidad semejante. De lo cual surge el siguiente enunciado de la Ley de las aceleraciones de la gravedad:
Los tiempos de oscilación de un mismo péndulo en distintos lugares de la Tierra son inversamente proporcionales a las raíces cuadradas de las aceleraciones de la gravedad.
Fórmula del tiempo de oscilación del péndulo:
Para poder obtener el tiempo de oscilación de un péndulo se aplica la siguiente expresión:
t: tiempo de oscilación;
l: longitud de péndulo;
g: aceleración de la gravedad
que equivale al período o tiempo de oscilación completa.
Si fuera el correspondiente para una oscilación simple, aplicamos:
Esta fórmula condensa en sí las cuatro leyes del péndulo. En efecto, observamos
2) Como tampoco figura el ángulo de amplitud, “el tiempo de oscilación es independiente de la amplitud”.
3) La 3ra. y 4ta. leyes están incluidas en el factor:
Las aplicaciones del péndulo son variadas. Las más importantes son:
a) Determinación de la aceleración de la gravedad.
Sabemos que:
Elevando al cuadrado miembro a miembro es:
y despejando g, es:
en esta igualdad es: numero pi (constante=3.1415), y l: medible fácilmente, T: se determina con un buen cronómetro.
Por lo que esta ultima expresión nos permite calcular con relativa facilidad la aceleración de la gravedad en un lugar determinado.
Esto constituye la aplicación científica de mayor importancia del péndulo. Para estas determinaciones se emplean péndulos reversibles, es decir, péndulos que pueden oscilar primero alrededor de un eje y después alrededor de otro. Colocado de tal modo que en cada una de esas posiciones el péndulo posea la misma longitud, y por lo tanto las oscilaciones son isócronas (igual tiempo de oscilación).
Así se logran valores de gran precisión. Se debe tener en cuenta en estas determinaciones la temperatura, amplitud de las oscilaciones y las influencias del rozamiento del aire y del soporte del péndulo.
El método de medición de g, con el péndulo, lo imaginó y expresó Huygens, y fue aplicado por el físico matemático Borda.
b) Determinación del movimiento de rotación de la Tierra
Si disponemos de un péndulo suspendido de un alambre como indica la figura, y procedemos a sacarlo de su posición de equilibrio, observaremos que el plano de oscilación del péndulo no varía al girar el alambre sostén.
Por tanto: El plano de oscilación de un péndulo se mantiene invariable al modificarse la posición del “plano sostén”. (figura abajo)
 Foucault, haciendo uso de esa propiedad, pudo demostrar la existencia del movimiento de rotación de la Tierra. Empleó un péndulo que constaba de una esfera de cobre de 25 kilogramos provista de un fiel y suspendida de la cúpula del Panteón (París) por medio de un alambre de acero de 79 m de largo.
Foucault, haciendo uso de esa propiedad, pudo demostrar la existencia del movimiento de rotación de la Tierra. Empleó un péndulo que constaba de una esfera de cobre de 25 kilogramos provista de un fiel y suspendida de la cúpula del Panteón (París) por medio de un alambre de acero de 79 m de largo.
En el suelo dispuso una capa de arena húmeda en la cual el fiel de la esfera pendular marcaba los trazos de sus oscilaciones.
Así se pudo ver que, a medida que transcurría el tiempo, esas marcas se iban modificando. Como el plano de oscilación es constante, significaba ello que lo variable era el plano del soporte, es decir, el Panteón o, lo que es igual, la Tierra. En realidad, este experimento puede realizarse en una sala ordinaria con péndulo más corto.
J. BI. Foucault: Físico francès, nacido y muerto en París (1819-68). Entre sus trabajos recordamos la invención del giroscopio, con el que puede determinarse la dirección del meridiano del lugar sin necesidad de la observación astronc5mica, el método para calcular la velocidad de la luz en el aire y en el agua, así como la demostración del movimiento de rotaciòn de la Tierra valiendose del pendulo.
Por tanto: El plano de oscilación de un péndulo se mantiene invariable al modificarse la posición del “plano sostén”. (figura abajo)
En el suelo dispuso una capa de arena húmeda en la cual el fiel de la esfera pendular marcaba los trazos de sus oscilaciones.
Así se pudo ver que, a medida que transcurría el tiempo, esas marcas se iban modificando. Como el plano de oscilación es constante, significaba ello que lo variable era el plano del soporte, es decir, el Panteón o, lo que es igual, la Tierra. En realidad, este experimento puede realizarse en una sala ordinaria con péndulo más corto.
J. BI. Foucault: Físico francès, nacido y muerto en París (1819-68). Entre sus trabajos recordamos la invención del giroscopio, con el que puede determinarse la dirección del meridiano del lugar sin necesidad de la observación astronc5mica, el método para calcular la velocidad de la luz en el aire y en el agua, así como la demostración del movimiento de rotaciòn de la Tierra valiendose del pendulo.
c) Medición del tiempo:
Huygens fue quien ideó un mecanismo para poder medir el tiempo. Sabemos que, para determinada longitud, el péndulo cumple una oscilación simple en un segundo. Por tanto, dando a un péndulo esa longitud, nos indicará, para cada oscilación, un tiempo igual a un segundo.
En otras palabras, si construimos un péndulo que efectúe en un día solar medio 86.400 oscilaciones, cada una de éstas nos indica un segundo.
Un péndulo que reúna estas condiciones, aplicado a un mecanismo motor (cuerda o pesas, que harán mover el péndulo) y a un sistema destinado a contar las oscilaciones, o sea, los segundos, constituye un reloj de péndulo.(figura izquierda)
En los relojes portátiles (de bolsillo, despertadores, etc.) el péndulo está reemplazado por el volante (rueda) que produce el movimiento oscilatorio del péndulo.
En otras palabras, si construimos un péndulo que efectúe en un día solar medio 86.400 oscilaciones, cada una de éstas nos indica un segundo.
Un péndulo que reúna estas condiciones, aplicado a un mecanismo motor (cuerda o pesas, que harán mover el péndulo) y a un sistema destinado a contar las oscilaciones, o sea, los segundos, constituye un reloj de péndulo.(figura izquierda)
En los relojes portátiles (de bolsillo, despertadores, etc.) el péndulo está reemplazado por el volante (rueda) que produce el movimiento oscilatorio del péndulo.
7. TIPOS DE CONVERSIÓN DE ENERGÍA
¿Qué significa que una magnitud física se conserva, en este caso la Energía Mecánica?
A lo largo de estas páginas hemos destacado que hay muchos tipos de energía. Nos hemos centrado en la energía potencial gravitatoria y la energía cinética. Ambas son características de un cuerpo en caída libre. Hemos comprobado que la suma de sus valores permanece constante. ¿Qué quiere decir esto exactamente? Pues que una magnitud física como la energía tiene la propiedad de transformarse, de unas formas en otras, de manera que la disminución de una supone el aumento de otra u otras.
El hombre se las ha ingeniado para aprovechar esta propiedad de la energía. Hemos desarrollado formas de transformar unas energías en otras más aprovechables: energía potencial gravitatoria en eléctrica, eléctrica en luminosa, energía química en calorífica...
En el caso de los fenómenos de caída libre sólo intervienen Ec. y Ep. y por tanto lo que aumenta/disminuye una, supone una disminución/aumento de la otra.
Las transformaciones de unas energías en otras es un fenómeno que se puede producir, en ciertos casos con facilidad. Algunos ejemplos son:
7.1. Energía potencial/cinética en eléctrica
7.2. energía eléctrica en potencial
8. ROZAMIENTO
La fuerza de rozamiento no realiza ningún trabajo útil. Sin embargo la expresión matemática del trabajo no distingue entre tipos de fuerzas. Podemos calcular el "trabajo perdido por rozamiento":
ANIMACIONES
¿Existe alguna relación entre el trabajo y la energía?
Presentamos la energía como la capacidad de un cuerpo de modificar su entorno. La palabra "modificar" incluye muchas cosas: iluminar, calentar,....moverse. El trabajo desarrollado por una fuerza es en último término producido por algún tipo de energía. Dicha energía se transforma en trabajo, de ahí que compartan la misma unidad de medida el Julio (J).
Presentamos la energía como la capacidad de un cuerpo de modificar su entorno. La palabra "modificar" incluye muchas cosas: iluminar, calentar,....moverse. El trabajo desarrollado por una fuerza es en último término producido por algún tipo de energía. Dicha energía se transforma en trabajo, de ahí que compartan la misma unidad de medida el Julio (J).
9.1. Experimento de Joule
En el experimento de Joule se determina el equivalente mecánico del calor, es decir, la relación entre la unidad de energía joule (julio) y la unidad de calor caloría.
Mediante esta experiencia simulada, se pretende poner de manifiesto la gran cantidad de energía que es necesario transformar en calor para elevar apreciablemente la temperatura de un volumen pequeño de agua.


Mediante esta experiencia simulada, se pretende poner de manifiesto la gran cantidad de energía que es necesario transformar en calor para elevar apreciablemente la temperatura de un volumen pequeño de agua.

La versión original del experimento, consta de dos pesas iguales que cuelgan simétricamente del eje.
La pesa, que se mueve con velocidad prácticamente constante, pierde energía potencial. Como consecuencia, el agua agitada por las paletas se clienta debido a la fricción.
Si el bloque de masa M desciende una altura h, la energía potencial disminuye en Mgh, y ésta es la energía que se utiliza para calentar el agua (se desprecian otras pérdidas).
Joule encontró que la disminución de energía potencial es proporcional al incremento de temperatura del agua. La constante de proporcionalidad (el calor específico de agua) es igual a 4.186 J/(g ºC). Por tanto, 4.186 J de energía mecánica aumentan la temperatura de 1g de agua en 1º C. Se define la caloría como 4.186 J sin referencia a la sustancia que se está calentando
1 cal = 4,186 J 1J = 0,24 cal.
En la simulación de la experiencia de Joule, se desprecia el equivalente en agua del calorímetro, del termómetro, del eje y de las paletas, la pérdida de energía por las paredes aislantes del recipiente del calorímetro y otras pérdidas debidas al rozamiento en las poleas, etc.
- Sea M la masa del bloque que cuelga y h su desplazamiento vertical
- m la masa de agua del calorímetro
- T0 la temperatura inicial del aguay T la temperatura final
- g=9.8 m/s2 la aceleración de la gravedad
Mgh=mc(T-T0)
Se despeja el calor específico del agua que estará expresado en J/(kg K).
Ejemplo:
Se introduce
Masa del bloque M=50 kg
Masa del agua en g (o volumen del agua en ml), m=100 g=0.10 kg
Altura h=1 m
Temperatura inicial T0=20ºC, y la temperatura final T=21.2ºC
Se introduce
Masa del bloque M=50 kg
Masa del agua en g (o volumen del agua en ml), m=100 g=0.10 kg
Altura h=1 m
Temperatura inicial T0=20ºC, y la temperatura final T=21.2ºC
ANIMACIONES


9.2. Máquina de vapor
La máquina de vapor es un motor de combustión externa que transforma la energía térmica contenida en el vapor de agua en energía mecánica.
El vapor de agua generado en una caldera cerrada produce la expansión del volumen de un cilindro, que empuja a un pistón. Mediante un balancín, el movimiento de subida y bajada del pistón del cilindro se transforma en un movimiento de rotación que acciona, por ejemplo, las ruedas de una locomotora o el rotor de un generador eléctrico.
Una vez alcanzado el final de la carrera, el émbolo retorna a su posición inicial y expulsa el vapor de agua.
9.3. Motor de combustión interna
Es una máquina que obtiene energía mecánica de la energía química producida por un combustible que arde dentro de una cámara de combustión.
Veamos a continuación el funcionamiento de un motor de cuatro tiempos.
1. Tiempo de admisión: el aire y el combustible mezclados entran por la válvula de admisión.
2. Tiempo de compresión: la mezcla aire/combustible es comprimida y encendida mediante la bujía.
3. Tiempo de combustión y expansión: el combustible se inflama y el pistón es empujado hacia abajo.
4. Tiempo de escape: los gases de escape se conducen hacia fuera a través de la válvula de escape.
Se ha visto en los apartados anteriores que el trabajo es una medida de los cambios producidos en los sistemas y que la energía es una medida de la capacidad para realizar trabajo. Trabajo y energía se miden en las mismas unidades, el joule en el S.I.
Pero hay un factor muy importante a tener en cuenta. Se trata del tiempo que se tarda en realizar un trabajo. De la relación entre el trabajo y el tiempo se ocupa una magnitud física conocida como potencia.
Potencia es el trabajo realizado dividido por el tiempo empleado en realizarlo:

En el S.I., su unidad es el Watt (W) o vatio que equivale a un joule por segundo (J/s). Un múltiplo suyo es el kiloWatt o kilovatio (1 kW = 1 000 W).
Por ejemplo, se realiza el mismo trabajo para subir un saco de 50 kg de arena a la azotea de un edificio tanto si se realiza en un minuto como si se tarda una hora, pero la potencia es mucho mayor en el primer caso.
También se usa la magnitud potencia para valorar la energía consumida por unidad de tiempo. Por ejemplo, una bombilla de 40 W consume una energía de 40 joules cada segundo.
|
| |
Un albañil sube desde la calle hasta la azotea de un edificio (a 20 m de altura) un saco de arena de 25 kg en 2 minutos mientras que una grúa es capaz de subir el mismo saco en un tiempo de 28 s hasta la misma azotea. Calcula la potencia desarrollada por la persona y por la máquina.
Primero, debemos calcular el trabajo necesario para subir un saco de arena hasta la azotea. Este trabajo será igual a la diferencia de energías potenciales del saco entre su posición a pie de calle y en la azotea.
W = Epf - Epi = m • g • hf - m • g • hi = 25 kg • 9,8 m/s2 • 20 m - 25 kg • 9,8 m/s2 • 0 m = 4900 J
Este trabajo es realizado en 2 minutos por el albañil y en 28 segundos por la grúa. La potencia desarrollada por uno y otra se calculan dividiendo por los tiempos respectivos:


11. RENDIMIENTO ENERGÉTICO
Unas formas de energía pueden transformarse en otras. En estas transformaciones la energía se degrada, pierde calidad. En toda transformación, parte de la energía se convierte en calor o energía térmica.
Cualquier tipo de energía puede transformarse íntegramente en calor; pero, éste no puede transformarse íntegramente en otro tipo de energía. Se dice, entonces, que el calor es una forma degradada de energía.
Se define, por tanto, el Rendimiento como la relación (en % por ciento) entre la energía útil obtenida y la energía aportada en una transformación.
12. ¿QUÉ ES EL CALOR?
Desde que los humanos dominaron el fuego, lo usaron para calentarse y cocer los alimentos, trabajar los metales o procurar reacciones químicas(Figura 20). Luego, el fuego puso en marcha las máquinas de vapor que iniciaron la revolución industrial. Este uso del calor para «trabajar» indica que el calor no es más que una forma de energía puesto que puede producir trabajo.
El primer científico que definió el calor como una forma de energía fue Benjamín Thomson al observar el calor generado al taladrar el agujero de los cañones en las fábricas de armamento.
El calor es una forma de energía y se mide por los efectos que produce.
Los efectos que produce el calor son de tres tipos: un aumento de la temperatura, un aumento del volumen y un cambio de estado físico.
Como energía que es, el calor se mide en joules (J) en el Sistema Internacional. Aún se usa la caloría (1 cal = 4,184 J) y sus múltiplos, como lakilocaloría (1 000 cal), especialmente para el valor energético de los alimentos.
Desde que los humanos dominaron el fuego, lo usaron para calentarse y cocer los alimentos, trabajar los metales o procurar reacciones químicas(Figura 20). Luego, el fuego puso en marcha las máquinas de vapor que iniciaron la revolución industrial. Este uso del calor para «trabajar» indica que el calor no es más que una forma de energía puesto que puede producir trabajo.
El primer científico que definió el calor como una forma de energía fue Benjamín Thomson al observar el calor generado al taladrar el agujero de los cañones en las fábricas de armamento.
El calor es una forma de energía y se mide por los efectos que produce.
Los efectos que produce el calor son de tres tipos: un aumento de la temperatura, un aumento del volumen y un cambio de estado físico.
Como energía que es, el calor se mide en joules (J) en el Sistema Internacional. Aún se usa la caloría (1 cal = 4,184 J) y sus múltiplos, como lakilocaloría (1 000 cal), especialmente para el valor energético de los alimentos.
Una caloría es la cantidadd ecalor que hay que dar a un gramo de agua para que su temperatura aumente en un grado
Como el calor es energía, cuando se aporta calor a un cuerpo ha de verse aumentada su energía. Ahora bien, si calentamos un ladrillo, no vemos que este ladrillo se mueva (cosa que representaría un aumento de energía cinética) ni que el ladrillo aumente su altura sobre el suelo (cosa que sería un aumento de energía potencial). Entonces, ¿dónde ha ido a parar la energía o el calor aportado? La respuesta está en la llamada energía interna de los cuerpos.
Como el calor es energía, cuando se aporta calor a un cuerpo ha de verse aumentada su energía. Ahora bien, si calentamos un ladrillo, no vemos que este ladrillo se mueva (cosa que representaría un aumento de energía cinética) ni que el ladrillo aumente su altura sobre el suelo (cosa que sería un aumento de energía potencial). Entonces, ¿dónde ha ido a parar la energía o el calor aportado? La respuesta está en la llamada energía interna de los cuerpos.
El calor que recibe un cuerpo se invierte en aumentar su energía interna.
| Esta energía interna no es más que la suma de toda la energía de las partículas que forman la materia del cuerpo en cuestión. O sea, la suma de las energías de traslación y de rotación de las moléculas en caso de gases y líquidos o de la energía de vibración en el caso de sólidos. Si un cuerpo absorbe calor, aumenta su energía interna y sus partículas se moverán más deprlsa. En cambio, si pierde calor, disminuye su energía interna y el movimiento de sus partículas será más lento y menos agitado |
Figura 21. El calor aumenta la energía interna de los cuerpos. Las moléculas de ese gas están más agitadas si la temperatura es mayor.
|
12.1. Las formas de transmisión de calor
La transmisión de calor puede darse por tres fenómenos: conducción, convección y radiación. La conducción es típica de sólidos. La convección es de líguidos y gases. La radiación se presenta en todos los estados físicos.
12.1.1. La conducción
Al calentar el extremo de una barra metálica, el calor llega al otro extremo al cabo de poco tiempo. Es un caso de conducción de calor. Así, ollas y sartenes transmiten por conducción el calor desde el fuego hacia su lado interior.
Es típica de los sólidos cuyos átomos, iones o moléculas no se pueden desplazar. Los átomos del extremo caliente vibran con más energía que los del extremo frío. Esta energía la comunican a los átomos vecinos, estos a sus vecinos de más allá y así, sucesivamente, la energía llega al otro extremo del sólido.
En la conducción, el calor se transmite por interacción entre átomos o moléculas sin que exista un transporte o desplazamiento neto de estos, o sea de materia.
La transmisión por conducción no es igual de efectiva en todas las sustancias:
Los buenos conductores permiten el paso rápido del calor a través suyo. Los metales son buenos conductores del calor (y también de la electricidad) y se usan para fabricar calderas, radiadores, cacharros de cocina, etc.
Los malos conductores o aislantes dificultan el paso del calor a través suyo. Por ejemplo, podemos introducir un extremo de un palo de madera en una hoguera sin quemarnos la mano por el otro extremo. Nuestros vestidos son aislantes del calor. Los abrigos, bufandas o guantes no nos dan calor pero evitan que escape el calor de nuestro cuerpo.
ANIMACIONES




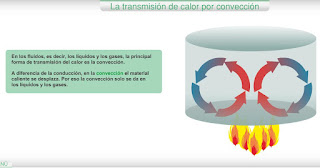
12.1.2. La convección
Al calentar agua en la cocina de casa se observan las sombras que se producen por la ascensión de moléculas calientes y descenso de las frías. Es un ejemplo de transferencia de calor por convección.
En la convección, el calor se transmite gracias al desplazamiento de átomos, moléculas o iones.
La transmisión de calor por convención. Se acompaña del movimiento de las partículas constituyentes.
La convección es típica de líquidos y gases. No se da en sólidos, pues las partículas que los forman no pueden desplazarse unas respecto a otras.
En el caso del aire, la capa en contacto con el suelo recibe su calor y se calienta dilatándose. Con ello, disminuye su densidad y asciende a través de capas de aire más frías y densas. La ascensión da un transporte de calor ligado al transporte del propio aire. Se crean las llamadas corrientes convectivas de aire caliente gue aprovechan las aves planeadoras y los pilotos de aviones sin motor y alas delta. A menor escala estas corrientes convectivas también se dan en el aire de una habitación y al calentar líguidos como agua en un cazo (Figura 23).
|
Figura 24. Convección producida al calentar agua en la vitrocerámica.
| ||
Figura 23. Tanto a nivel de toda la atmósfera como de una habitación, la transmisión de calor se produce por corrientes convectivas de aire.
| ||
ANIMACIONES



12.1.3. La radiación
Son ejemplos de la transmisión por radiación tanto el calor que nos llega de una estufa como el calor del Sol que nos llega desde 150 millones de kilómetros sin que entre él y la Tierra haya ningún medio material.
En la transmisión por radiación el calor se propaga sin necesitar la ayuda de materia
La energía calorífica se transmite por ondas electromagnéticas. (Son las radiacciones infrarrojas).
Las radiaciones electromagnéticas son ondas que viajan tanto a través de la materia como del vacío. Entre ellas, la luz visible, los rayos ultravioleta, los rayos infrarrojos, los rayos X, las ondas de radio y televisión y las microondas.
Todos los cuerpos, solo por tener una temperatura, emiten radiación electromagnética. La cantidad de energía que irradia un cuerpo depende:
de su temperatura,
del área del cuerpo expuesta al entorno (Figura 25).
Los radiadores de automóvil o de calefacción se diseñan en forma de láminas para aumentar su superficie. Algunos animales como los elefantes eliminan calor por las grandes superficies de sus orejas.
13. LOS EFECTOS DEL CALOR
Tabla 3.1. Calor específico de algunas sustancias.
| El calor aumenta la energía interna de un cuerpo y produce tres efectos físicos:
13.1. La variación de la temperaturaEs el efecto más inmediato de los intercambios de calor entre los cuerpos.
|
| No todos los cuerpos tienen la misma facilidad para aumentar o disminuir de temperatura cuando reciben o pierden calor. Esto depende delcalor específico (Tabla 1), que es una propiedad de cada cuerpo y mide su facilidad para calentarse o enfriarse. Se define calor específico como l a cantidad de calor que hay que suministrar a la unidad de masa de una sustancia o sistema termodinámico para elevar su temperatura en una unidad (kelvin o grado Celsius). La ecuación que relaciona la cantidad de calor, Q, con la masa de un cuerpo, m, y su calor específico, C y la variación de temperatura, ∆T = Tf - Ti. es:
Q = m • c • (Tf - Ti )
El calorímetro es el aparato de medida que permite calcular el valor del calor específico de cada sustancia.
Se dilatan y contraen tanto los sólidos como los líquidos y los gases. Se define: Dilatación. Aumento de volumen debido al aumento de temperatura. Contracción. Disminución de volumen por la bajada de temperatura. Todos los cuerpos y sustancias se dilatan al aumentar su temperatura y se contraen al disminuir su temperatura. Sólo una se comporta de una forma distinta: el agua. De 100 °C hasta 4 °C disminuye de volumen si desciende la temperatura y aumenta si asciende esta, pero entre 4 °C y 0 °C al disminuir la temperatura se da un ligero aumento del volumen. Además, el agua al pasar de líquida a sólida aumenta de volumen. La menor densidad permite al hielo flotar sobre el agua líquida. La densidad máxima del agua se alcanza a 4 ºC. En la dilatación de sólidos pueden darse los siguientes casos:
En la dilatación de líquidos:
|
Para sólido, líquido y gas, los cambios de estado se resumen en (Figura 28):
- Fusión es el paso de sólido a líquido. Solidificación es el paso inverso. Se producen a una temperatura concreta llamada temperatura de fusión.
- Evaporación es el paso de líquido a gas a cualquier temperatura.
- Condensación es el paso inverso también a cualquier temperatura.
- Ebullición es el paso de líquido a gas a la temperatura de ebullición.
- Licuación es el paso inverso también a esta temperatura determinada.
- Sublimación es el paso directo de sólido a gas sin pasar por líquido.Sublimación inversa o regresiva es el paso directo de gas a sólido. Ambos solo se dan en algunas sustancias, por ejemplo, el yodo o el alcanfor.
- Fusión, evaporación, ebullición y sublimación son procesos que transcurren con absorción de calor, por lo que aumenta la temperatura. Son procesos llamados progresivos.
- Solidificación, condensación, licuación y sublimación inversa son procesos en los que se libera calor, por lo que desciende la temperatura. Son procesos llamados regresivos.
Mientras se produce el cambio de estado la temperatura del cuerpo no cambia. Todo el calor aportado se invierte en el cambio de estado. Lo mismo ocurre si el cambio es regresivo. Entonces, el calor se desprende y la temperatura de la sustancia tampoco varía hasta que acaba el cambio de estado físico.


Este calor necesario para el cambio de estado recibe el nombre de calor latente.
Así, se habla del calor latente de fusión, Lf y del calor latente de vaporización , Lv. Su valor es distinto para cada sustancia pues no todas cambian de estado con la misma facilidad. Son propiedades específicas, ya que dependen de cada sustancia.
La Tabla 2 da algunos de estos valores en unidades del S.I. Se calcula el calor para fundir, Qf , o vaporizar , Qv , una cantidad de una sustancia multiplicando el valor de los calores latentes, Lf o Lv, de esta sustancia por la masa, m, de la sustancia en cuestión:
Qf = Lf • m Qv = Lv • m
Para procesos de solidificación y de licuación sirven las mismas fórmulas y los mismos calores latentes, pero el signo del calor será negativo, si se desprende.
En la siguiente tabla, se proporcionan los datos referentes a los cambios de estado de algunas sustancias.
Tabla 2. Calores latentes de algunas sustancias. |
Supuesto práctico 10
Se quieren calentar 85 litros de agua desde 20 °C hasta 65 °C. Calcula el calor que se necesitará suministrar:
La densidad del agua es de 1 kg/L. Con ello, 85 L eguivalen a 85 kg, y para hacer problemas de calor (termodinámica), se deben usar grados Kelvin que se hallan sumando a los grados Celsius la cantidad de 273, aunque al hayar una diferencia de temperaturas, la cantidad será igual en grados celsius que en grados kelvin.
T1 = 273 + 20 ºC = 293 K y T2 = 273 + 65 ºC = 338 K; T2-T1 = 338 K - 293 K = 45 K
Aplicando: Q = m • C • (T2-T1)
Q = 85 kg • 4,18 J/kg.K •(65 °C - 20 °C) = 85 kg • 4,18 J/kg·K • 45 °C = 415 988,5 J, según el libro. No debe haber grados celsius (ºC).
Q = 85 kg • 4,18 J/kg.K •(338 K - 293 K) = 85 kg • 4,18 J/kg·K • 45 K = 415 988,5 J, así debe hacerse.
Supuesto práctico 11
Calcula el calor necesario para fundir 250 kg de hielo (calor latente de fusión del hielo = 333,9 kJ/kg).
Qf = Lf • m = 333,9 kJ/kg • 250 kg = 83 475 kJ
El calor que recibe un cuerpo se invierte en aumentar su energía interna, que es la suma de todas las energías de traslación y de rotación de las moléculas en caso de gases y líguidos o de las energías de vibración en el caso de sólidos.
Si un cuerpo absorbe calor, aumenta su energía interna y sus partículas se moverán más deprisa.Pero si pierde calor, disminuye su energía interna y el movimiento de sus partículas será más lento y menos agitado. La temperatura es una medida, en promedio, de esta agitación:
La temperatura mide la agitación de las partículas que forman un cuerpo.
La temperatura de un sistema material es proporcional a la energía cinética media de sus partículas.
A mayor temperatura, mayor agitación de los átomos o moléculas que forman un cuerpo. Si se conoce la temperatura de dos cuerpos, puede predecirse si pasará calor de uno a otro cuando puedan interactuar (Figura 3.27):
Si dos cuerpos que tienen distinta temperatura se ponen en contacto, pasará calor del que tiene mayor temperatura al que tiene menos.
Cuando dos cuerpos tienen la misma temperatura, no hay flujo de calor entre ellos y se dice que están en equilibrio térmico.
A mayor temperatura, mayor agitación de los átomos o moléculas que forman un cuerpo. Si se conoce la temperatura de dos cuerpos, puede predecirse si pasará calor de uno a otro cuando puedan interactuar (Figura 3.27):
Si dos cuerpos que tienen distinta temperatura se ponen en contacto, pasará calor del que tiene mayor temperatura al que tiene menos.
Cuando dos cuerpos tienen la misma temperatura, no hay flujo de calor entre ellos y se dice que están en equilibrio térmico.
| Figura 29. Si dos cuerpos a distinta temperatura pueden interactuar, pasa calor del más caliente (T1) al más frío (T2) hasta que se igualan sus temperaturas (equilibrio térmico). | |
Se mezclan 10 L de agua a 20 °C con 6 L de agua a 60 °C. Calcula la temperatura de la mezcla.
T(K) = t (ºC) + 273; 20ºC son 273 +20 K, es decir 293 K y 60 ºC serán 273 + 60 K; es decir, 333 K
De la ecuación de arriba sale: t (º C) = T (K) - 273
El calor cedido (- Q) por el agua callente debe ser igual al captado (+Q) por el agua fría. Siendo T la temperatura final desconocida para ambas masas de agua. Si se aplica Q = m • c • (T-Ti), a ambas masas:
En grados Celsius, ºC:
Calor ganado por el agua a 20 ºC: Q = m • c • (T-Ti) = 10 kg • c • (T- 20 °C)
y es igual que el calor perdido por el agua a 60 ºC: - Q = - m • c • (T-Ti) = - 6 kg • c • (T- 60 °C)
Y ahora se iguala, queda:
10 kg • c • (T- 20 °C) = - 6 kg • c • (T- 60 °C)
No es necesario sustituir el calor específico del agua por su valor pues se anula en ambos lados de la Igualdad.
La Igualdad: 10 T - 200 = -6 T + 360.
Despejando queda: 16 T = 560. De donde T = (560 / 16) ºC= 35 °C.
En termodinámica se debe trabajar con grados Kelvin, K, aunque el resultado debe ser el mismo:
Calor ganado por el agua a 293 K: Q = m • c • (T-Ti) = 10 kg • c • (T- 293 K)
Y ahora se iguala, queda:
10 kg • c • (T- 20 °C) = - 6 kg • c • (T- 60 °C)
No es necesario sustituir el calor específico del agua por su valor pues se anula en ambos lados de la Igualdad.
La Igualdad: 10 T - 200 = -6 T + 360.
Despejando queda: 16 T = 560. De donde T = (560 / 16) ºC= 35 °C.
En termodinámica se debe trabajar con grados Kelvin, K, aunque el resultado debe ser el mismo:
Calor ganado por el agua a 293 K: Q = m • c • (T-Ti) = 10 kg • c • (T- 293 K)
es igual que el calor perdido por el agua a 333 K: - Q = - m • c • (T-Ti) = - 6 kg • c • (T- 333 K)
Y ahora se iguala, queda:
10 kg • c • (T- 293 K) = - 6 kg • c • (T- 333 K)
No es necesario sustituir el calor específico del agua por su valor pues se anula en ambos lados de la Igualdad.
La Igualdad: 10 T - 2930 = -6 T + 1998
Despejando queda: 16 T = 4928. De donde T = (4928 / 16) K= 308 K;
t (º C) = T (K) - 273 = 308 K - 273 = 35 °C.
Supuesto práctico 13
Se mezclan 50 kg de agua a 17 °C con 18 kg de alcohol (etanol)a 40 °C. Calcula la temperatura final de la mezcla. Los calores específicos para el agua y para el etanol son 4,18 kJ/kg • K y 2,4 kJ/kg • K , respectivamente.
T(K) = t (ºC) + 273; 17 ºC son 273 +17 K, es decir 290 K y 40 ºC serán 273 + 40 K; es decir, 313 K
De la ecuación de arriba sale: t (º C) = T (K) - 273
Calor ganado por el agua a 17 ºC:
Y ahora se iguala, queda:
10 kg • c • (T- 293 K) = - 6 kg • c • (T- 333 K)
No es necesario sustituir el calor específico del agua por su valor pues se anula en ambos lados de la Igualdad.
La Igualdad: 10 T - 2930 = -6 T + 1998
Despejando queda: 16 T = 4928. De donde T = (4928 / 16) K= 308 K;
t (º C) = T (K) - 273 = 308 K - 273 = 35 °C.
Supuesto práctico 13
Se mezclan 50 kg de agua a 17 °C con 18 kg de alcohol (etanol)a 40 °C. Calcula la temperatura final de la mezcla. Los calores específicos para el agua y para el etanol son 4,18 kJ/kg • K y 2,4 kJ/kg • K , respectivamente.
T(K) = t (ºC) + 273; 17 ºC son 273 +17 K, es decir 290 K y 40 ºC serán 273 + 40 K; es decir, 313 K
De la ecuación de arriba sale: t (º C) = T (K) - 273
Calor ganado por el agua a 17 ºC:
Qagua = magua • cagua • (T-Ti) = 50 kg • 4,18 kJ/kg · K • (T- 17 °C);
y es igual que el calor perdido (signo "-") por el etanol a 40 ºC:
- Qetanol = - metanol • cetanol • (T-Ti) = - 18 kg • 2,4 kJ/kg · K • (T- 40 °C)
magua • cagua • (T-Ti) = - metanol • cetanol • (T-Ti);
Sustituyendo los valores, en º C:
50 kg • 4,18 kJ/kg · K • (T- 17 °C) = - 18 kg • 2,4 kJ/kg · K • (T- 40 °C);
209 • (T -17 ºC ) = - 43,2 • (T- 40 °C)
209 T -2553 = - 43,2 T + 1728
209 T + 43,2 T = 1728 + 2553;
252,2 T = 4281; T = (5281/252,2) ºC = 20,94 ºC
50 kg • 4,18 kJ/kg · K • (T- 290 K) = - 18 kg • 2,4 kJ/kg · K • (T- 313 K);
209 • (T - 290 K) = - 43,2 • (T- 313 K)
209 T - 60610 = - 43,2 T + 13521,6
Despejando:
209 T + 43,2 T = 13521,6 + 60610 ;
252,2 T = 74131,6; T = (74131,6/252,2) K = 293,94 K
Comprobando: t (º C) = T (K) - 273 = 293,94 K -273 =20,94 ºC
Para medir la temperatura se miden propiedades de los cuerpos que varíen con ella.
Por ejemplo, la longitud de un hilo metálico, la presión de un gas o el volumen de un líguido. Los aparatos que miden la temperatura son los termómetros (Figura 3.28) y están calibrados en alguna de las escalas de temperatura (Figura 3.29). De las diversas escalas de temperatura gue se han establecido, dos son las gue han arraigado más:
14.1.1. Escala Celsius o centígrada
- Debida al sueco Anders Celsius toma como base dos puntos fijos:
- La temperatura de congelación del agua como punto inferior 0 °C.
- La temperatura de ebullición del agua como punto superior, 100 °C.
- Se tomó el grado centígrado como la centésima parte de esta diferencia.
- Su símbolo es °C. Por ejemplo: 0 °C, 36 °C, 100 °C. Las temperaturas más bajas que la de congelación del agua se consideran negativas: -4 °C, -30 °C, etc.
Daniel Gabriel Fahrenheit (1686-1736) era un físico Alemán que inventó el termómetro de Alcohol en 1709 y el termómetro de mercurio en 1714. La escala de temperatura Fahrenheit fue desarrollada en 1724. En la escala Fahrenheit, el punto de congelación del agua es de 32ºF (grados Fahrenheit), y el de ebullición es de 212ºF (grados Fahrenheit). Una diferencia de 1,8 grados Fahrenheit equivale a una diferencia de 1 grado Celsius. La temperatura del cuerpo humano es 98,6ºF. Se usa mucho en los EEUU y Gran Bretaña.
Daniel Gabriel Fahrenheit, lo hizo así: "Colocando el termómetro en una mezcla de sal de amonio o agua salada, hielo y agua, encontré un punto sobre la escala al cual llamé cero. Un segundo punto lo obtuve de la misma manera, si la mezcla se usa sin sal. Entonces denoté este punto como 30. Un tercer punto, designado como 96, fue obtenido colocando el termómetro en la boca para adquirir el calor del cuerpo humano." No debía estar muy bien ese día.
14.1.3. Escala kelvin o absoluta
Creada por el británico William Thomson que fue nombrado «lord Kelvin»:
Su cero o cero absoluto es la temperatura más baja posible del Universo. En ella, hasta el movimiento de los átomos y de sus electrones se detendría.
Como el cero absoluto es la temperatura más baja posible, en la escala absoluta no hay temperaturas negativas.
Se mide en unidades kelvin, iguales al grado Celsius, es decir un grado Kelvin es igual que un grado Celsius. . Aumentar un grado Celsius (centígrado) de temperatura es lo mismo que aumentar o disminuir un kelvin.
Es la unidad de temperatura del Sistema Internacional, su símbolo es K (nunca °K) y su nombre no es el de «grado kelvin» sino simplemente «kelvin».
Escala Internacional de temperaturas
Desde 1990, las escalas kelvin y centígrada quedaron unificadas en una sola escala que admite como unidades de medida tanto el kelvin como el grado centígrado. La equivalencia entre ambas unidades de medida es:
T (K) = t (°C) +273,15
Así, 0 K corresponde a -273,15 °C y 0 °C corresponde a 273,15 K. (Este curso podremos usar 273, como equivalencia)
Para pasar una temperatura de una a escala a otra es usan las siguientes fórmulas:
| De | a | Fórmula |
| Fahrenheit | Celsius | t (ºC) = ( t (ºF) - 32 ) / 1,8 |
| Celsius | Fahrenheit | t (ºF) = 1,8 · t (ºC) + 32 |
| Celsius | Kelvin | T (K) = t (ºC) + 273 |
| Kelvin | Celsius | t (º C) = T (K) - 273 |
La temperatura corporal en una persona sana es 36,5 °C. Exprésala en temperatura absoluta o kelvin:
t = 36,5 °C que, en kelvin, es: T= (36,5 + 273,15) K= 309,65 K; o T(K) = t (ºC) + 273 = 36,5 + 273 = 309,5 K
Supuesto Práctico 15
La temperatura de congelación del mercurio es 234,32 K (-38,68°C) y su temperatura de ebullición es de 629,88 K. Exprésalas en grados Celsius.
T(K) = t (ºC) + 273; de donde: t (º C) = T (K) - 273
Tcongelación = 234,32 K
tcongelación= (234,32 - 273,15) °C = -38,83 °C; o tcongelación= (234,32 - 273) °C = -38,68 °C
Tebullición = 629,88 K
tebullición = (629,88 - 273,15) °C = 356,73 °C ; o tebullición = (629,88 - 273) °C = 356,88 °C
15.1. Palancas
Para levantar un tonel puedes hacerlo "a pulso", pero seguro que te va a costar mucho esfuerzo. ¿No habrá formas más cómodas de hacerlo?
Una posible solución es “hacer palanca”: ponemos un punto de apoyo cerca del peso y aplicamos
una fuerza hacia abajo lejos de él.
Cuanto más alejados estemos del punto de apoyo, menor será la fuerza que tendremos que hacer.

|
 La palanca es una máquina simple que transmite la fuerza que se aplica en un punto a otro punto en el que se obtiene una fuerza mayor.
La palanca es una máquina simple que transmite la fuerza que se aplica en un punto a otro punto en el que se obtiene una fuerza mayor.
ANIMACIONES
 15.2. Poleas
15.2. Poleas Además de la palanca, existen otras máquinas simples que nos pueden ayudar a levantar un peso sin demasiado esfuerzo. Una de ellas es la polea.
| ||||||
La polea es una máquina simple que nos puede ayudar a subir pesos ahorrando esfuerzo. Cuando un sistema está formado por poleas fijas y poleas móviles, se llama polipasto.
El polipasto está formado por un conjunto de poleas. Cuando una es fija y las demás móviles tenemos un polipasto del tipo I, cuando la mitad son fijas y la otra mitad móviles tenemos un polipasto del tipo II. La fuerza "F" necesaria para levantar una carga "R" siendo "n" el número de poleas móviles, se determina, en cada caso, con una de las fórmulas:
ANIMACIONES
El polipasto está formado por un conjunto de poleas. Cuando una es fija y las demás móviles tenemos un polipasto del tipo I, cuando la mitad son fijas y la otra mitad móviles tenemos un polipasto del tipo II. La fuerza "F" necesaria para levantar una carga "R" siendo "n" el número de poleas móviles, se determina, en cada caso, con una de las fórmulas:
Polipasto tipo I
| |
Polipasto tipo II
|
ANIMACIONES
La relación cinemática entre dos ruedas dentadas con números de dientes z1 y z2 y velocidades de giro n1 y n2 en rpm, así como su relación de transmisión, i, se determina con las fórmulas:
Con las ruedas dentadas el movimiento se puede transmitir entre árboles paralelos (ruedas rectas y helicoidales); entre árboles que se cortan (ruedas cónicas); y entre árboles que se cruzan perpendicularmente (sinfín corona).
15.4. Ruedas de fricción
La transmisión con ruedas de fricción se produce entre discos lisos en contacto por su periferia. Debido a la elevada presión entre las ruedas y al alto coeficiente de rozamiento del material se transmite movimiento circular desde la rueda motriz o de entrada a la rueda de salida. El sentido de giro de la rueda conducida es contrario al de la motriz. Su principal inconveniente es que no pueden transmitir grandes potencias porque patinarían.En el punto de contacto entre las dos ruedas la velocidad es la misma para ambas si consideramos que no hay deslizamiento, de aquí, se deduce la relación cinemática del movimiento entre dos ruedas, donde "d1" y "d2" son los diámetros de las ruedas y "n1" y "n2" los números de revoluciones.
La transmisión por poleas y correa se realiza por fricción, empleamos la correa para unir dos ruedas que llamamos poleas, el sentido de giro de la polea de salida es el mismo que el de la motriz. Si queremos transmitir grandes potencias con la correa lisa tenemos que utilizar varias en paralelo si no patinarían. Para evitar deslizamientos se usan correas dentadas o cadenas, con estos elementos conseguimos transmitir grandes esfuerzos y una relación de transmisión exacta. Igual que en las ruedas de fricción la relación cinemática es:
15.6. Piñón cremallera
Un mecanismo piñón cremallera está formado por una rueda dentada que engrana con una barra también dentada. Es un mecanismo que transforma el movimiento circular de la rueda en rectilíneo de la cremallera o viceversa. Se emplea para dar movimiento, por ejemplo, a carros de máquinas, bandeja de un lector de CD, eje principal de un taladro, etc.
La relación de movimiento entre rueda y cremallera, llamando "az" al desplazamiento de la cremallera por diente de la rueda y, "av" al desplazamiento de la cremallera por vuelta de la rueda, será:
La relación de movimiento entre rueda y cremallera, llamando "az" al desplazamiento de la cremallera por diente de la rueda y, "av" al desplazamiento de la cremallera por vuelta de la rueda, será:
15.7. Tornillo tuerca Este mecanismo consta de un tornillo y una tuerca que tienen como objeto transformar el movimiento circular en rectilíneo. Si hacemos girar el tornillo o la tuerca manteniendo la orientación del otro, el que no gira avanza según la fórmula:
Siendo "p" el paso del tornillo y "n" el número de vueltas. Este mecanismo tiene muchas aplicaciones en desplazamientos lineales lentos: portales automáticos, prensas, tornillos de banco, carros de máquinas, etc.  15.8. Biela manivela Este mecanismo está formado por una manivela que tiene un movimiento circular y una barra llamada biela que está unida con articulaciones por un extremo a la manivela y por otro a un sistema de guiado (pistón) que describe un movimiento rectilíneo alternativo. El mecanismo es reversible, el movimiento de entrada tanto puede ser circular de la manivela como rectilíneo alternativo de la guía de la biela. El sistema biela manivela tiene mucha importancia en los motores de explosión alternativos, así como antes también lo tuvo en la construcción de máquinas de vapor.  15.9. Excéntrica El mecanismo de excéntrica consta básicamente de dos elementos, la propia excéntrica y el seguidor. La excéntrica es un disco cilíndrico que tiene un eje de giro desplazado un valor "e", llamado alzada, respecto del centro del disco. El seguidor es una varilla que está en contacto permanente con la excéntrica y que recibe el movimiento de esta. Con este ingenio conseguimos transformar el movimiento circular de la excéntrica en movimiento rectilíneo alternativo del seguidor. El mecanismo no es reversible. La forma de la gráfica del movimiento descrito por el extremo del seguidor es la misma para cualquier excéntrica, solo varía la amplitud del movimiento, lo que llamamos alzada (e).  15.10. Leva El mecanismo de leva y seguidor se emplea para transformar el movimiento circular en un movimiento rectilíneo alternativo con unas características determinadas que dependen del perfil de la leva. La forma de la leva se diseña según el movimiento que se pretende para el seguidor. Para saber las características del movimiento del seguidor es necesario realizar una gráfica. En los motores de combustión alternativos se emplean levas para efectuar la apertura y cierre de las válvulas que dejan entrar el combustible y salir los gases de la cámara de combustión. Las levas pueden tener distintas formas, de disco, cilíndricas y de campana; la más común es la de disco.  Identifica cada una de las máquinas
Ampliación
16. RESUMEN
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
18. CUESTIONES




19. VÍDEOS






















































































No hay comentarios:
Publicar un comentario