ESQUEMAS
PRESENTACIONES





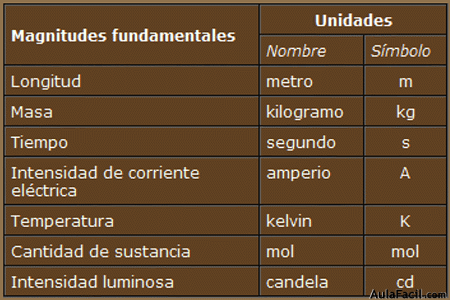
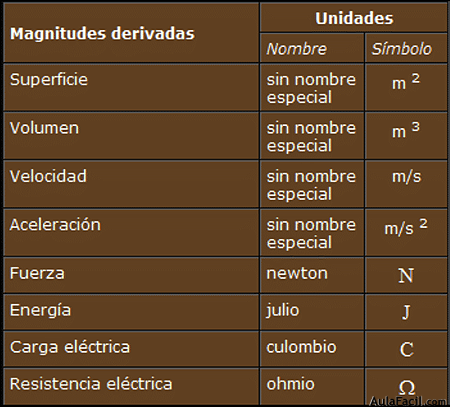
Definición de las unidades de las magnitudes fundamentales del SI
Barras de error
El trabajo en el laboratorio
OTROS CONTENIDOS
La Medida
LABORATORIO
Lectura- densidad, desde Arquímedes hasta el Titanic
EJERCICIOS

Tabla para los Factores de Conversión
Cambios de unidades - Hoja nº 1
Cambios de unidades - Hoja nº 2
Cambios de unidades - Hoja nº 3
Cambios de unidades - Hoja nº 4
Cambio de unidades 1
Cambio de unidades 2
Ejercicio 1
Ejercicio 2
Ejercicio 3
Ejercicios del Método Científico y cálculo de errores
Tratamiento de datos
PRÁCTICAS
Como trabajan los científicos
VÍDEOS
La Medida
LABORATORIO
CIENTÍFICOS E INVENTOS
Ficha- Hieron II y Arquímedes
Ficha- historia de un farmacéutico
Ficha- la alquimia en la edad media
Ficha- la ballena cabeza de melón
Ficha- material de laboratorio
Ficha- MC Beriberi
Ficha- MC Dirac y la poesía
Ficha- MC el detective y el científico
Ficha- MC la peste negra
Ficha- MC niño en una isla perdida
Ficha- resuelta-introducción al método científico
Ficha- el método científico
Ficha- ejercicios de razonamiento
Ficha- introducción a la ciencia
Ficha- lectura referida a Arquímedes
Lámina- como se mide el tiempoFicha- historia de un farmacéutico
Ficha- la alquimia en la edad media
Ficha- la ballena cabeza de melón
Ficha- material de laboratorio
Ficha- MC Beriberi
Ficha- MC Dirac y la poesía
Ficha- MC el detective y el científico
Ficha- MC la peste negra
Ficha- MC niño en una isla perdida
Ficha- resuelta-introducción al método científico
Ficha- el método científico
Ficha- ejercicios de razonamiento
Ficha- introducción a la ciencia
Ficha- lectura referida a Arquímedes
Lectura- densidad, desde Arquímedes hasta el Titanic
EJERCICIOS

Tabla para los Factores de Conversión
Cambios de unidades - Hoja nº 1
Cambios de unidades - Hoja nº 2
Cambios de unidades - Hoja nº 3
Cambios de unidades - Hoja nº 4
Cambio de unidades 1
Cambio de unidades 2
Ejercicio 1
Ejercicio 2
Ejercicio 3
Ejercicios del Método Científico y cálculo de errores
Ejercicios de medida
Ejercicios 4
Ejercicios de cambio de unidades
Ejercicios método científico y la medida
Unidades 1
Unidades 2
Unidades 3
Unidades 4
Unidades 5
Densidad 1
Densidad 2
Ejercicios 4
Ejercicios de cambio de unidades
Ejercicios método científico y la medida
Ficha- cambio de unidades
Ficha- las magnitudes y su medida
Ficha- magnitudes y unidades
Ficha- magnitud física y su medida
Ficha- las magnitudes y su medida
Ficha- magnitudes y unidades
Ficha- magnitud física y su medida
Unidades 2
Unidades 3
Unidades 4
Unidades 5
Densidad 1
Densidad 2
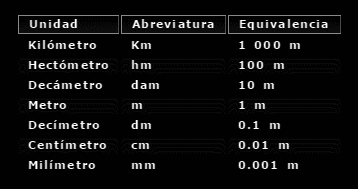
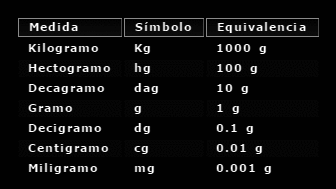
| Transformación de unidades de longitud Transformación de unidades de superficie Transformación de unidades de volumen Instrumentos de medida Glosario |
| 3. La medida | VER EJERCICIOS |
| 4. Instrumentos de medida | VER EJERCICIOS |
| 5. Errores | VER EJERCICIOS |
| 6. Medidas directas e indirectas | VER EJERCICIOS |
| 8. Ordenación y clasificación de datos | VER EJERCICIOS |
| 9. El trabajo en las ciencias experimentales: el método científico | VER EJERCICIOS |
| 10. Actividades | VER EJERCICIOS |
PRÁCTICAS
| Ángulos Aprende a medir ángulos con el transportador. | Balanza monoplato Mide la masa de cada uno de los matraces. Ejercicios para aprender a utilizar la balanza monoplato. | ||
| Calibre Seis tipos de calibre para aprender a medir el diámetro interior, el diámetro exterior y la profundidad de diferentes piezas. | Escalas termométricas Relación entre las escalas Celsius, Fahrenheit y Kelvin. |
Como trabajan los científicos
VÍDEOS

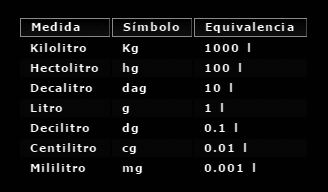
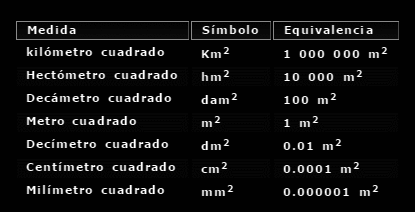
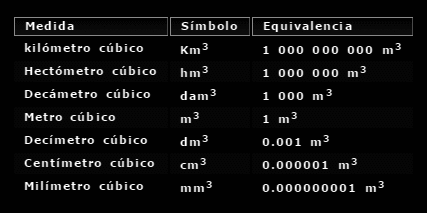


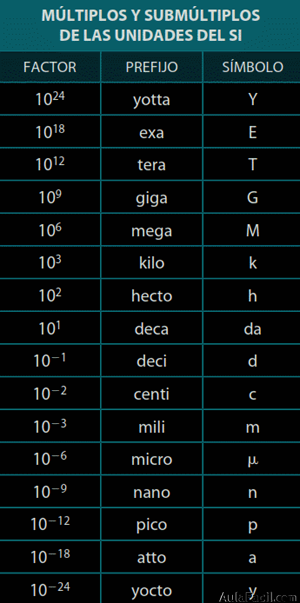


No hay comentarios:
Publicar un comentario